Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 27
Calcule o valor da integral múltipla.
ondeestá acima do plano , abaixo do plano e dentro do cilindro .
Passo 1
E aí, tudo bom com vocês?
Vamos lá, nessa questão precisamos calcular a integral
de acordo com a região dada.
Para isso, vamos usar coordenadas cilíndricas pra reescrever nossa integral como uma integral iterada:
Depois disso, vamos calcular a integral, de dentro pra fora.
Passo 2
A região de integração é dada por:
está acima do plano , abaixo do plano . Daqui já sabemos que:
Além disso, está dentro do cilindro
Vamos desenhar isso:
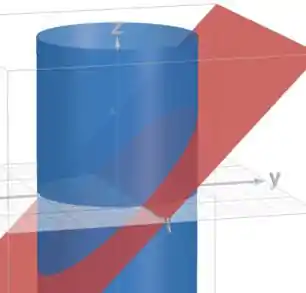
Em vermelho, temos o plano , que pra desenhar basta fazer a reta no plano e estender para o .
Em azul é o cilindro , que é uma circunferência no plano estendida ao longo de .
Assim, o sólido está entre essas duas superfícies, acima do plano ():
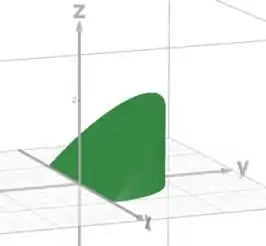
Como nosso sólido é parte de um cilindro, podemos usar coordenadas cilíndricas.
Passo 3
Pra achar os limites de e , vamos olhar pra projeção desse sólido no plano :
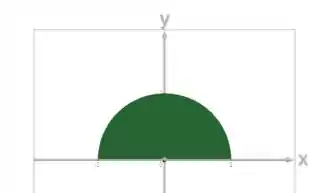
Como estamos dentro de um círculo de raio (limitado por ):
E como estamos só na parte acima do eixo :
Reescrevendo os limites de :
Assim, nossa integral pode ser reescrita de forma iterada como sendo
Passo 4
Bom, vamos começar a integrar, de dentro pra fora.
Primeiro em função de , mantendo e constantes:
Como é constante em função de , pode sair dessa primeira integral:
Então:
Passo 5
Agora, como nossos limites de integração são constantes, e conseguimos separar nosso integrando em funções de cada uma das variáveis, a gente pode separar a integral em um produto de integrais simples:
Vamos resolver a primeira integral, primeiro mudando :
E agora fazemos uma substituição :
Então:
Calculando:
A segunda integral calculamos direto:
Então: