Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 41
Utilize coordenadas polares para calcular
Passo 1
Faala, galera!
Nessa questão, precisamos calcular uma integral...
Só que ela deu a integral em coordenadas cartesianas e pediu pra usarmos coordenadas polares!
Primeiro vamos relembrar as coordenadas polares.
Bom, nossas variáveis deixam de ser e e passam a ser e , dessa forma:
Sem nos esquecer do jacobiano que é para essa mudança de variável.
Então pra resolver, a gente vai começar olhando pra região de integração (a partir dos limites de e da integral original), assim conseguimos achar os limites de integração das variáveis novas.
E ai fazemos a mudança de variáveis e calculamos a integral!
Passo 2
Os limites de integração da integral que a função deu nos dão isso aqui:
Isso quer dizer que o domínio de integração está entre as curvas:
Se a gente elevar os dois lados ao quadrado, descobrimos que na verdade são duas partes da mesma curva:
Que é uma circunferência centrada na origem e de raio . A equação com “” representa a parte abaixo do eixo (), e a outra representa a parte de cima.
Como o varia entre e , sabemos que estamos só na parte positiva de . Assim conseguimos desenhar o domínio:
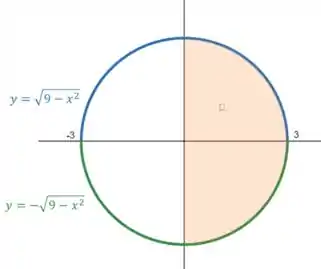
Em coordenadas polares, como estamos num círculo de raio , o varia até , e como estamos à direita do eixo , o varia de e :
Agora olhando pro nosso integrando, vamos mudar ele pra coordenadas polares:
Da relação trigonométrica , temos que
Então
Então nossa integral fica:
Passo 3
Agora vamos começar a integrar, de dentro pra fora.
Primeiro, integramos em função de . Nesse caso, consideramos como uma constante!
Como é constante em função de , podemos tirar dessa primeira integral:
Aplicando nos limites de integração:
Como é constante, pode sair da integral, e integramos em função de :
Calculando nos limites:
Então: