Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 16
Esboce o sólido cujo volume é dado pela integral e calcule-a.
Passo 1
Faaala, pessoal!
Essa questão pede pra gente esboçar o sólido que essa integral representa o volume, depois calcular.
Percebe que essa integral está em coordenadas cilíndricas, e o integrando é o próprio jacobiano , então essa integral é a mesma coisa que:
Que representa o volume do sólido , que é o domínio de integração.
Então o que vamos fazer pra esboçar é olhar pros limites de integração das coordenadas cilíndricas:
Primeiro vamos olhar pra coordenada , e depois as outras duas , que vão ser equivalentes a coordenadas polares no plano .
Depois de esboçar, vamos calcular a integral, de dentro pra fora.
Passo 2
Os limites de são:
Ou seja, o sólido está entre (plano ) e , que é um cone. A gente consegue confirmar isso trocando esse por coordenadas cartesianas:
Lembra que é sempre positivo! Então:
Que é a equação do cartesiana de um cone.
Já vimos, então, que o sólido está entre essas duas superfícies:
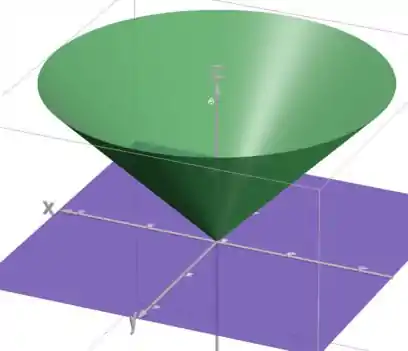
Olhando agora pra projeção do sólido no plano , pelas outras duas coordenadas:
Esses limites representam exatamente um disco de raio :
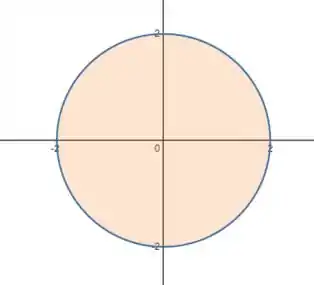
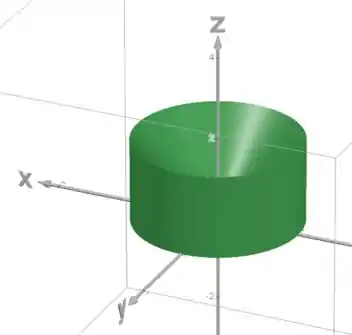
Vamos colocar tudo no pra conseguirmos esboçar o sólido:
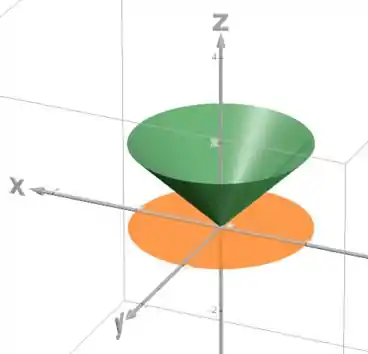
O sólido fica assim:
Passo 3
Pra calcular a integral iterada, vamos integrar de dentro pra fora.
Primeiro, em função de , considerando e constante:
Calculando nos limites:
Agora integramos em função de , com constante:
Substituindo nos limites:
Finalmente, integramos em função de :
Então:
Resposta
