Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.9 - Ex. 1 -b
Faça um esboço do gráfico e indique os seguimentos de reta cujos comprimentos são dy e
Passo 1
Do exercício a) obtemos
Sabendo que dy =
Passo 2
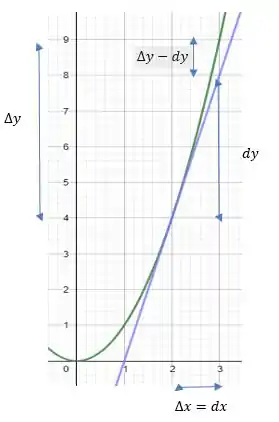
A Curva verde é nossa função y = x² . A curva Azul é a reta tangente ao ponto x = 2, onde usamos pra inclinação dessa reta a aproximação de Taylor , ou seja , 2= 4
Podemos ver que o é o incremento real da nossa função . E o dy nossa aproximação por diferenciais.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos Exercícios 19-38, determine d y .31- y = e x
Nos Exercícios 19-38, determine d y .28- y = s e c ( x 2 - 1 )
Nos Exercícios 19-38, determine d y .21- y = 2 x 1 + x 2
Nos Exercícios 19-38, determine d y .25- y = s i n ( 5x )
Nos Exercícios 19-38, determine d y .23- 2 y 3 2 + x y - x = 0