Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 16
Use uma calculadora ou um computador para fazer uma tabela dos valores das somas e e de Riemann à esquerda e à direita para a integral com , , e 100. Entre quais dois números o valor da integral deve ficar? Você pode fazer uma afirmação análoga para a integral ? Explique.
Passo 1
Fala pessoal, nessa questão temos que realizar a soma de Riemann pela esquerda e pela direita para encontrar o valor da seguinte integral:
E vamos usar como subintervalos os valores e .
Aqui podemos usar uma calculadora programável, dessa forma, não vamos precisar fazer contas de verdade.Mas vamos lembrar o que a soma de Riemann representa:
Ela é o cálculo da área de retângulos que são feitos em subintervalos do intervalo total. A altura do retângulo é o valor da função em um ponto do subintervalo e a base do retângulo é o comprimento do subintervalo, de forma que temos o seguinte somatório:
Com
Onde é o número de subintervalos. é o comprimento de cada subintervalo e são os extremos do intervalo total.
é um valor de que pertence ao subintervalo. Na soma a direita, esse valor é escolhido como sendo o extremo direito do subintervalo e na soma a esquerda, esse valor é escolhido como sendo o extremo esquerdo do subintervalo.
Por fim, devemos indicar entre quais dois números o valor da integral deve ficar.
Passo 2
Vamos começar criando uma tabela com os valores para a soma de Riemann pela esquerda e pela direita com os subintervalos pedidos:
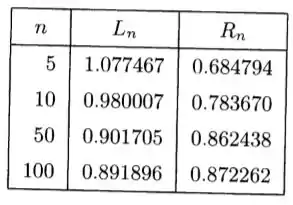
Usando a melhor aproximação, que é a com retângulos, o valor da integral deve estar entre e .
Vemos portanto que a aproximação pela esquerda deu uma superestimativa e a aproximação pela direita deu uma subestimativa.
Passo 3
Nós não podemos fazer afirmação análoga para a integral , porque é crescente de a .
E quando temos uma função crescente, a aproximação pela esquerda é uma subestimativa e pela direita é uma superestimativa, o que é ao contrário do que ocorre na função entre e .
Resposta
O valor da integral deve estar entre e . Não podemos fazer uma afirmação análoga.