Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 70
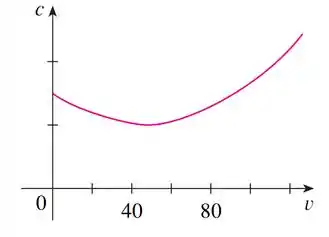
O gráfico mostra o consumo de combustível de um carro (medido em litros/hora) como uma função da velocidade do carro. Em velocidade muito baixa, o motor não rende bem; assim, inicialmente decresce à medida que a velocidade cresce. Mas em alta velocidade o consumo cresce. Você pode ver que é minimizado para esse carro quando . Porém, para a eficiência do combustível, o que deve ser minimizado não é o consumo em litros/hora, mas, em vez disso, o consumo de combustível em litros por quilômetro. Vamos chamar esse consumo de . Usando o gráfico, estime a velocidade na qual tem seu valor mínimo.
Passo 1
Falaii galerinha do Responde ai, tudo belezinha?
A questão pede para determinar a velocidade na qual o consumo de combustível em litros por quilômetro é minimizado.
O gráfico fornecido mostra o consumo de combustível em litros por hora em função da velocidade do carro.
Já sabemos que é minimizado em , mas o que precisamos minimizar é o consumo de combustível em litros por quilômetro.
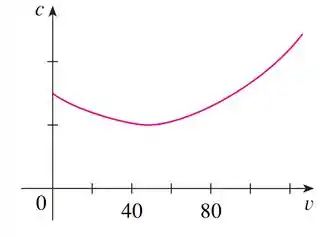
Para encontrar a velocidade que minimiza precisamos entender a relação entre
- é o consumo em litros por hora.
- é o consumo em litros por quilômetro.
A relação entre pode ser dada por:
Isso ocorre porque é o consumo por hora, e para converter para consumo por quilômetro, dividimos pelo número de quilômetros percorridos em uma hora, que é a própria velocidade
Passo 2
Como vamos relacionar o que foi dado com o que está pedindo?
Simboraa...
- O gráfico mostra em função de
- Precisamos usar a relação
para determinar onde é mínimo.
Identificação da função
- Observando o gráfico, vemos que tem um ponto mínimo em .
Expressão para
- A expressão para é:
Minimização de
- Para minimizar , precisamos derivar em relação a e igualar a zero.
Ou seja, queremos encontrar:
Passo 3
Cálculo da derivada:
- A derivada de em relação a é:
- Usando a regra do quociente:
- Para minimizar igualamos a derivada a zero:
Passo 4
Análise gráfica e resultado:
- A análise gráfica do comportamento de indica que é minimizado em
- No entanto, queremos mínimo.
Como
Devemos verificar os valores próximos de
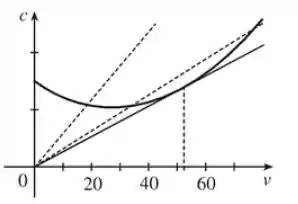
Conclusão:
- Para , calcule
- Observando a forma do gráfico e a análise da derivada, estimamos que a velocidade que minimiza está levemente superior a provavelmente em torno de
Portanto, a velocidade na qual o consumo de combustível em litros por quilômetro tem seu valor mínimo é aproximadamente
“O coelho está certo, e ele é claramente o mais inteligente entre vocês!”
Resposta
Portanto, a velocidade na qual o consumo de combustível em litros por quilômetro tem seu valor mínimo é aproximadamente