Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 3.1 - Ex. 8l

Calcule o volume do conjunto dado. (Sugerimos ao leitor desenhar o conjunto.)

Passo 1

Pelo teorema de Fubini, tem-se que o volume de um conjunto é dado por

V = ∫ ∫ B f x ,   y d x d y

Ou:

V = ∫ a b ∫ c y d y f x ,   y d x d y = ∫ c d ∫ a x b x f x ,   y d y d x

Onde f x ,   y = z .

Neste caso, z é limitada por duas funções e, logo, o volume é definido pela diferença entre elas.

Além disso, B é dado no enunciado pela inequação x 2 + y 2 ≤ 2 x que representa uma circunferência de raio r = 1 . Observando o esboço do conjunto:

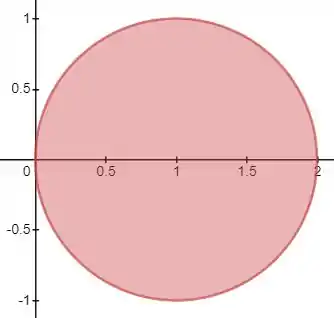
Os limites de integração podem ser dados por:

0 ≤ x ≤ 2

E, o valor de y será determinado neste caso por:

x 2 - 2 x + y 2 ≤ 0

Completando quadrados:

x 2 - 2 x + 1 + y 2 ≤ 1 → x - 1 2 + y 2 ≤ 1

- 1 - x - 1 2 ≤ y ≤ 1 - x - 1 2

Ou:

- 1 ≤ y ≤ 1

E, para determinar o valor de x neste caso:

x 2 - 2 x + y 2 = 0 → x = 2 ± 4 - 4 y 2 2 = 1 ± 1 - y 2

1 - 1 - y 2 ≤ x ≤ 1 + 1 - y 2

Passo 2

Logo, o volume será dado por:

V = ∫ 0 2 ∫ - 1 - x - 1 2 1 - x - 1 2 2 x - ( x 2 + y 2 ) d y d x

V = ∫ 0 2 2 ∫ 0 1 - x - 1 2 2 x - x 2 - y 2 d y d x

Resolvendo a integral em relação à y :

V = 2 ∫ 0 2 2 x y - x 2 y - y 3 3 | y = 1 - x - 1 2 y = 0 d x

Substituindo o intervalo de integração:

V = 2 ∫ 0 2 2 x 1 - x - 1 2 - x 2 1 - x - 1 2 - 1 - x - 1 2 3 3 d x

V = 2 ∫ 0 2 2 x - x 2 1 - x - 1 2 - 1 3 1 - x - 1 2 1 - x - 1 2 d x

V = 2 ∫ 0 2 2 x - x 2 1 - x - 1 2 - 1 3 2 x - x 2 1 - x - 1 2 d x

V = 4 3 ∫ 0 2 2 x - x 2 1 - x - 1 2 d x

Passo 3

Agora, integrando em relação à x , o problema pode ser resolvido através do método da substituição simples, com x - 1 = s e n u e d x = c o s u d u .

Também, fazendo as substituições tem-se que:

Quando x = 2 → u = π / 2

Quando x = 0 → u = - π / 2

Então:

V = 4 3 ∫ - π / 2 π / 2 2 1 + s e n u - 1 + s e n u 2 1 - s e n 2 u c o s u   d u

V = 4 3 ∫ - π / 2 π / 2 2 + 2 s e n u - 1 + 2 s e n u + s e n 2 u c o s u c o s u   d u

V = 4 3 ∫ - π / 2 π / 2 1 - s e n 2 u c o s u c o s u   d u

V = 4 3 ∫ - π / 2 π / 2 c o s 4 u d u

Utilizando a identidade trigonométrica

c o s 2 n x = 1 + cos ⁡ 2 n x 2

A integral pode ser reescrita como:

V = 4 3 ∫ - π / 2 π / 2 1 + cos ⁡ 2 u 2 2 d u

V = 4 3 1 4 ∫ - π / 2 π / 2 1 + 2 cos ⁡ 2 u + c o s 2 2 u d u

Fazendo uma substituição novamente:

V = 1 3 ∫ - π / 2 π / 2 1 + 2 cos ⁡ 2 u + 1 + cos ⁡ 4 u 2 d u

V = 1 3 ∫ - π / 2 π 2 3 2 + 2 cos ⁡ 2 u + cos ⁡ 4 u 2 d u

V = 1 3 3 2 u + s e n 2 u + s e n 4 u 8 | u = π / 2 u = - π / 2

Passo 4

Substituindo o intervalo de integração, todos os termos que possuem a função e resultem em s e n n π serão nulos. Portanto:

V = 1 2 π 2 - - π 2

V = π 2

Resposta

π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral trocando a ordem de integração. ∫ 0 1∫ 3 y 3 e x 2 d x d y
Calcule a integral trocando a ordem de integração. ∫ 0 1∫ x 2 1 y sin ⁡ y d y d x
Calcule a integral trocando a ordem de integração. ∫ 0 8∫ y 3 2 e x 4 d x d y
Expresse D com a união de regiões do tipo I ou do tipo I I e calcule a integral. ∬ D x 2 d A
Expresse D com a união de regiões do tipo I ou do tipo I I e calcule a integral. ∬ D y d A