Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.1 - Ex. 65

Calcule o volume gerado pela rotação da região delimitada pelas curvas y = l n x , y = 0 e x = 2 em torno de cada eixo.

O eixo y ;

O eixo x .

Passo 1

Beleza, amigo? A questão nos pede e nós iremos aqui calcular o volume de uma região que rotaciona em torno de um eixo.

Primeiro, vamos ver qual é a região. Esse gráfico foi gerado utilizando o GeoGebra.

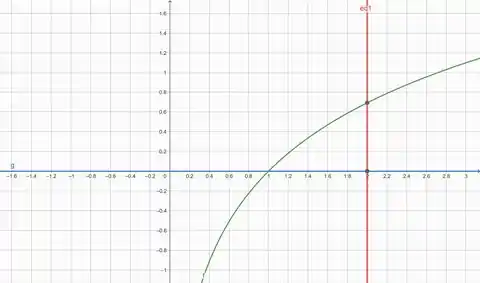
Na letra (a) vamos calcular o volume com a rotação em relação ao eixo y . Vamos aqui usar o método das cascas. O volume é dado por:

V = ∫ a b 2 π x f x d x

Passo 2

Substituindo na integral, temos:

V = ∫ 1 2 2 π x ln ⁡ x d x

Vamos resolver essa integral pelo método de integração por partes, pois aqui temos um produto de funções para integrar e esse metodo é muito bom para essas situações!

Seja u = l n x     → d u = d x / x e d v = x d x     → v = x 2 / 2 . Vamos escrever como fica a integral

A integral por partes é:

∫     u d v = u v - ∫     v d u

Utilizando a nossa substituição:

V = 2 π 1 2 x 2 l n x 1 2 - ∫ 1 2 1 2 x d x

Passo 3

Vamos resolver a integral!

V = 2 π 2 ln ⁡ 2 - 0 - 1 4 x 2 1 2

V = 2 π 2 l n 2 - 3 4

Passo 4

Agora na letra (b) vamos calcular o volume com a rotação em relação ao eixo x .Vamos aqui suar o método dos discos. O volume é dado por:

V = ∫ a b π f x 2 d x

Substituindo na integral, temos:

V = ∫ 1 2 π l n x 2 d x

Vamos resolve essa integral novamente pela integração por partes! Seja u = l n x 2     → d u = 2 l n x x d x e d v = d x     → v = x . Vamos escrever como fica a integral:

V = π { x l n x 2 1 2 - ∫ 1 2 2 l n x d x

Passo 5

Vamos resolver a integral!

V = π { x l n x 2 1 2 - ∫ 1 2 2 l n x d x

A integral que temos acima também não é tão fácil de resolver. Vamos aplicar o método da substituição de variável aqui. Seja u = l n x       → d u = d x x e d v = d x   → v = x . Assim,

V = π 2 l n 2 2 - 2 x l n x 1 2 - ∫ 1 2 d x

V = π { 2 l n 2 2 - 4 l n 2 + 2 x 1 2

V = π 2 l n 2 2 - 4 l n 2 + 2

V = 2 π [ l n 2 2 - 2 l n 2 + 1 ]

Resposta

V = 2 π 2 l n 2 - 3 4   ;

V = 2 π [ l n 2 2 - 2 l n 2 + 1 ] .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o exercício 47 para encontrar int (ln x)^3 d x .
Suponha que f 1 = 2 , f 4 = 7 , f ' 1 = 5 , f ' 4 = 3 e que f ' ' seja contínua. Determine o valor de ∫ 1 4 xf ' ' xd x .
Uma partícula que se move ao longo de uma reta tem velocidade igual a v t = t 2 e - t metro por segundo após t segundos. Qual a distância que essa partícula percorrerá durante os t primeiros segundos?
Se f (0) = g (0) = 0 e f ' ' e g ' ' são contínuas, mostre queint_0^a f (x) g ' ' ( x ) = f (a) g^' (a) - f^' (a) g (a) + int_0^a f^(' ') (x) g (x) d x
Calcule a integral.int x cos^2 x d x