Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.2 - Ex. 1h
Calcule o volume do sólido obtido pela rotação, em torno do eixo , do conjunto de todos os pares (x,y), tais que :
e
Passo 1
Nessa questão temos três inequações, então faremos três gráficos e a interseção. Com isso, veremos melhor as informações importantes!
Sem mais enrolação, vamos começar pelo que nos dará a direção, dá uma olhadinha nesses gráficos que estão aqui embaixo:
Inicialmente iremos fazer um esboço dos gráficos das figuras da questão:
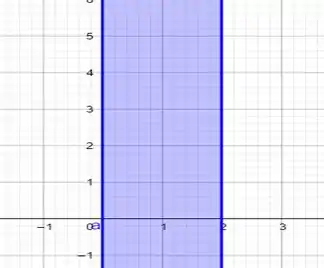
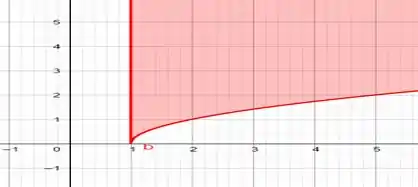
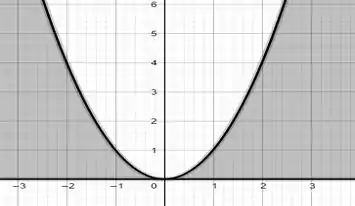
E agora da interseção entre esses dois gráficos, que está em verde:
Passo 2
Faremos a diferença entre os volumes determinados pela funções
Chamaremos de , o volume determinado pela função e o limite de integração será de
Chamaremos de , o volume determinado pela função e o limite de integração será de
Deixarei nossa fórmula aqui, caso você tenha esquecido hein!!!
Passo 3
Calcularemos :
Calcularemos
A integral acima não é imediata, para fazermos iremos chamar de
Substituiremos todas as informações acima dentro da integral:
Voltando para a variável inicial, temos isso aqui ó:
Com a integral indefinida já calculado, com certo suor kkk, faremos a definida agora:
Ufaaaa, estamos terminando, só mais um poquinho! Tome seu café e vamos lá!