Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.1 - Ex. 1c

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que :

4 e

Passo 1

A integração será um problema pequeno comparado a visualização, então preste bastante atenção nos gráficos, eles serão nossa bússola em problemas de volume de figuras rotacionadas.

Sem mais enrolação, vamos começar pelo que nos dará a direção, dá uma olhadinha nesses gráficos que estão aqui embaixo:

Inicialmente iremos fazer um esboço dos gráficos das figuras da questão:

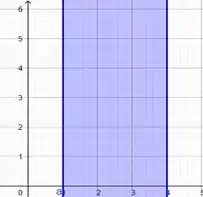
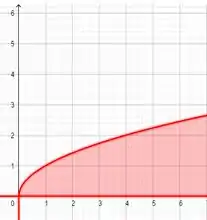
E agora a interseção entre esses dois gráficos de verde!

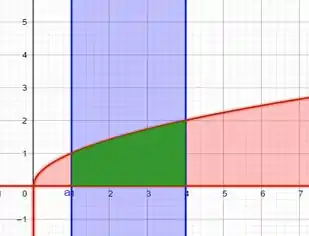
Passo 2

Para calcular o volume do sólido rotacionado em torno do eixo x, temos que analisar qual é a interseção e qual os intervalos de integração, que serão as retinhas que delimitam a figura de interseção.

Nesse problema você pode dar uma olhada e vai perceber que é para

Caso tenha esquecido, tá aí a fórmula:

Passo 3

Nosso intervalo de integração será, e a função

Não esqueça, devemos elevar ao quadrado, pois é ela a parte de “dentro” da integral:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do sólido obtido pela rotação, em torno do eixo x , do conjunto de todos os pares ( x , y ) , tais que : 1 ≤ x ≤ 3 e 0 ≤ y ≤ x

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : y ≥ x 2ex 2 + y 2 ≤ 2

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : 2 x 2 + y 2 ≤ 1 e y ≥ 0

(Teorema de Papus para a elipse.) Considere que o conjunto A de todos os pontos (x,y) tais que ( x - α ) 2 a 2 + y - β 2 b 2 ≤ 1a ≥ 0eb ≥ 0 e situado no semiplano y ≥ 0 . Mostre que o volume do sólido