Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.1 - Ex. 1i

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que :

y ≥ x 2   e   x 2 + y 2 ≤ 2

Passo 1

Faremos os gráficos das duas curvas e veremos como proceder nessa questão:

Inicialmente iremos fazer um esboço dos gráficos das figuras da questão:

y ≥ x 2

x 2 + y 2 ≤ 2

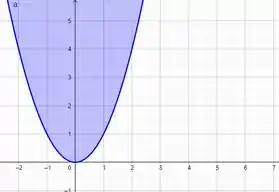
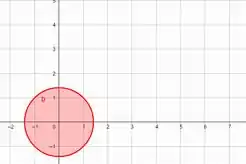
Interior de uma circunferência de raio =   2 e centro (0,0)

E agora a interseção entre esses dois gráficos de verde, e a reta x = 1 , para facilitar a visualização tanto da região que será importante no problema quanto nos limites de integração:

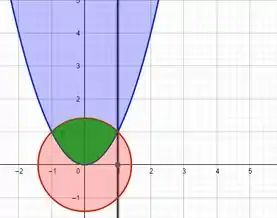
Passo 2

Faremos inicialmente uma análise do gráfico para extrairmos as coisa importantes, vamos lá:

Percebemos que essa figura é simétrica em relação ao eixo y, mas no que isso ajuda? Só é mais uma coisa para eu lembrar? Não, meu caro colega.

Poderemos fazer a integral com os limites de 0 até 1 e depois multiplicar por 2, ao invés de fazermos de -1 até 1. É bem melhor utilizarmos o 0 no limite de integração né.

Faremos o seguinte, vem comigo, chamaremos V 1 do volume delimitado pelos pontos x 2 + y 2 ≤ 2 com limites de integração de 0 até 1, lembra da simetria????

E chamaremos de V 2 o volume delimitado pelos pontos y ≥ x 2 com os mesmo limites de integração de 0 até 1 pelo mesmo motivo de cima hein.

E o volume que queremos é a subtração de V1-V2 e depois multiplicamos por 2, última vez que falo, mas multiplicamos por 2, por conta da simetria, pronto não falo mais.

Passo 3

Paraaa, paraaaa. Leia com a voz do João Kleber. Você se lembra da fórmula do volume? Não? Então está aí, meu amigo:

V = π ∫ y 2 d x

Agora faremos o V1   ( y 2 = 2 - x 2 ) :

π ∫ 0 1 2 - x 2 d x = π   ( 2 ∫ 0 1 d x - ∫ 0 1 x 2 d x ) = π ( 2 x 1 0 - x 3 3 1 0 ) = 5 π 3

Faremos V2 ( y 2 = x 4 ) :

π ∫ 0 1 x 4 d x = π x 5 5 1 0 = π 5

Faremos a diferença entre os volumes e depois multiplicaremos por 2, depois que fizermos isso game over questão:

V = 2 ( V 1 - V 2 ) = 2 5 π 3 - π 5 = 44 π 15

Resposta

V = 44 π 15

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : 0 ≤ y ≤ xex 2 + y 2 ≤ 2
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : y ≥ 0 ,1 ≤ x ≤ 2ex 2 - y 2 ≥ 1
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : 0 ≤ x ≤ 1 e x ≤ y ≤ 3
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : 0 ≤ x ≤ 8 e 0 ≤ y ≤ x 3
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : 1 ≤ x ≤ 2 e 0 ≤ y ≤ x 2 - 1