Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.1 - Ex. 1l
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que :
Passo 1
Faremos três gráficos das funções do problema e mais o gráfico de interseção entre as funções.
Mas por que faríamos três?
Simplesmente porque está definido entre duas funções e faremos um gráfico para cada lado da inequação.
Vamos lá, vem tranquilo e sem afobação:
Inicialmente iremos fazer um esboço dos gráficos das figuras da questão:
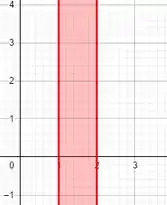
Lembrando que esse é apenas o lado esquerdo da inequação, temos que fazer o lado direito
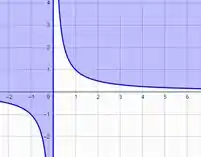
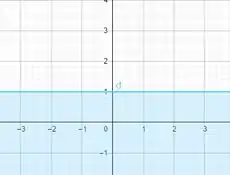
E agora faremos a interseção entre todos eles, e será representado de verde.
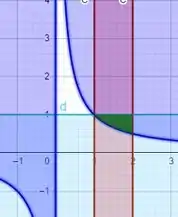
Passo 2
Para calcular o volume do sólido rotacionado em torno do eixo x, temos que analisar qual é a interseção e qual os intervalos de integração, que serão as retinhas que delimitam a figura de interseção entre os gráficos:
Nesse problema você pode dar uma olhada e vai perceber que é para
O volume nessa questão vai ser dado pela diferença entre , volume delimitado por , e , volume delimitado por .
Caso tenha esquecido a fórmula de calcular, aí está:
Passo 3
Vamos começar com :
Intervalo de integração de :
Agora vamos para :
Com intervalo de integração de :
Estamos quase acabando, mas não se distraía agora, depois de tanto trabalho temos que acertar uma questão dessa! Faremos a diferença entre esses dois volumes e teremos acabado!