Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.1 - Ex. 1d
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que :
e
Passo 1
A integração será um problema pequeno comparado a visualização, então preste bastante atenção nos gráficos, eles serão nossa bússola em problemas de volume de figuras rotacionadas.
Sem mais enrolação, vamos começar pelo que nos dará a direção, da uma olhadinha nesses gráficos que estão aqui em baixo:
Inicialmente iremos fazer um esboço dos gráficos das figuras da questão:
Atenção: É o interior de uma elipse de centro e eixo maior em (0,1) e eixo menor (,0) em x.
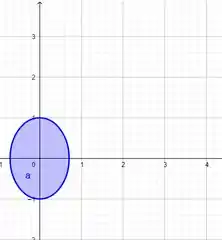
É apenas a região positiva de y, porém manteremos o costume de sempre fazer os gráficos, lembre-se nessas questões os gráficos são nossa bússola:
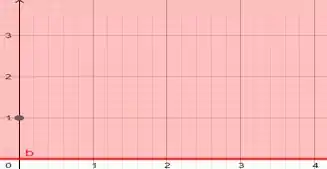
E agora a interseção entre esses dois gráficos, que estará representado de Verde!
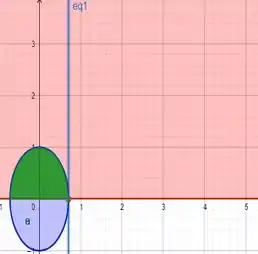
Passo 2
Algo muito importante a ser percebido é que essa figura é simétrica em relação ao eixo , dá uma olhada, e como isso facilitaria nosso trabalho, meu caro amigo?
Ora, não iremos integrar entre os dois limites que seriam: e , mas sim entre os limites: e e depois multiplicaremos por 2.
Vamos concordar integrar com limite de integração é muito melhor né???
Antes de ir pro próximo passo, a fórmula do volume:
Passo 3
Outra coisa importante em elipses e depois veremos que em circunferências também ocorrem é que queremos ou para botar na nossa fórmula do volume e a elipse assim como a circunferência, já nos dá isso. Como?????
Assim, ó:
Substituindo na nossa fórmula e lembrando que nosso intervalo de integração será de a ,temos isso aqui:
Quebrando a nossa integral em duas:
Lembra da simetria? Caso não lembre da uma passadinha no passo 2.
E você que lembra, temos que fazer o que?
Simplesmente multiplicar por :