Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 48
Tente esboçar à mão a intersecção do cilindro parabólico com a metade superior do elipsoide . Escreva então as equações paramétricas para a curva e utilize um computador para traçá-la.
Passo 1
E aí, pessoal? Primeiro, vamos tentar determinar as equações paramétricas da curva.
Se estamos falando de intersecção, então devemos achar equações paramétricas que possam satisfazer as equações das duas superfícies. Vamos começar com o cilindro parabólico:
Uma boa parametrização pra esse cilindro é:
Após isso, nós iremos utilizar essa parametrização em:
E assim iremos encontrar a parametrização para . Para esboçar, iremos utilizar o GeoGebra, mas você pode utilizar o Desmos, ou outro software gráfico.
Passo 2
Agora, para o elipsoide, devemos ter:
Substituindo a parametrização que a gente encontrou no passo 1:
Para achar uma equação paramétrica pra , poderíamos ter dois valores ao tirar a raiz quadrada, um positivo e um negativo. Como o enunciado nos falou em metade superior do elipsoide, pegaremos a raiz positiva:
Então, as equações paramétricas da curva de intersecção serão:
Passo 3
Agora, vamos utilizar um computador pra desenhar as duas superfícies e termos uma ideia de como é a curva de intersecção entre elas:
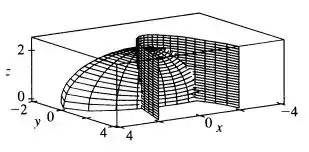
E utilizando as equações paramétricas já encontradas, vamos efetivamente desenhar a curva, beleza?
