Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 33
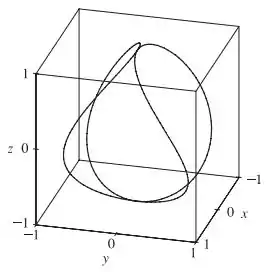
Utilize um computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva.
Passo 1
Eaee, belezinha?? Bom.. queremos utilizar uma ferramenta gráfica para esboçar a seguinte curva vetorial:
Assim, deveremos analisar o seu domínio para entender a natureza da curva.
Para isso, deveremos procurar alguma restrição que faça com que a equação não exista (divisão por zero, raiz de números negativos, indeterminações em geral).
Agora bora lá!! 😉
Passo 2
Analisando as equações paramétricas da curva, temos:
Não há restrições para que essa curva não exista. Assim, o domínio são todos os números reais!!
Assim, temos a seguinte figura:
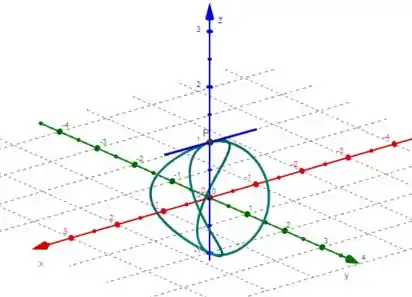
Obs: desconsidere o ponto e sua tangente.
Como todas as funções componentes são compostas de senos ou cossenos, podemos ter certeza que a curva está contida no cubo :
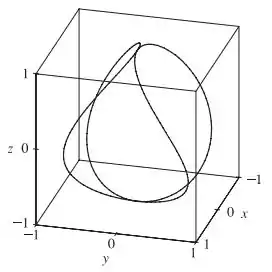
Para uma outra visualização, podemos fazer tipo um tubo em volta da curva:
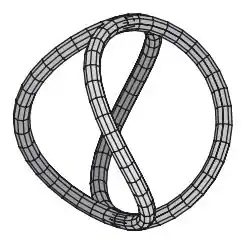
Resposta
