Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.1 - Ex. 32
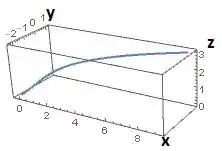
Utilize um computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva.
Passo 1
Fala ai pessoal. De boa? Vamos resolver essa questãozinha? Aqui temos a equação vetorial:
E queremos fazer o seu gráfico! Pra isso devemos escolher um domínio do parâmetro e ponto de vista de forma que as principais características da curva fiquem visíveis!
Essa é bem tranquila, até porque temos que apenas utilizar um software para resolve-lá!
Então vamos fazer o seguinte, vamos entender está função e como o gráfico ficará.
Vamos lá!
Passo 2
Vamos interpretar os termos.
A coordenada descreve uma parábola abrindo para cima no plano .
A coordenada descreve uma curva que cresce lentamente para à medida que aumenta.
A coordenada descreve uma linha reta ao longo do eixo .
Passo 3
Com o passo 2, já sabemos como será a nossa curva. Mas vamos entender os intervalos?
O exercício pede para plotarmos com auxílio do computador a curva dada pela equação vetorial
Como pelo domínio da curva e o é uma função crescente de , escolher um intervalo pequeno como é bem razoável:
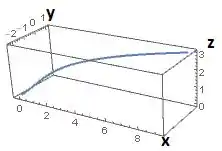
Resposta
