Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.4 - Ex. 31

Cardioide no primeiro quadrante: Encontre a área da região cortada do primeiro quadrante pela cardioide r   =   1   +   s e n ( θ ) .

Passo 1

Faaaala, cara! Tranquileba?

Fazendo um esboço do gráfico, temos:

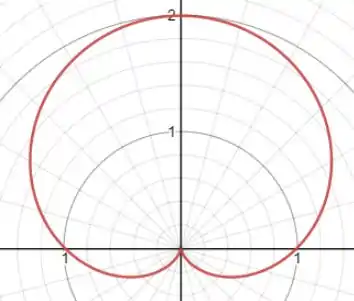
Vejamos que:

0 ≤ θ ≤ π 2

E dado que:

0 ≤ r ≤ 1 + s e n θ

Logo:

A = ∫ 0 π 2 ∫ 0 1 + s e n θ r   d r   d θ

Passo 2

∫ 0 π 2 1 2 r 2 0 1 + s e n θ d θ

1 2 ∫ 0 π 2 1 + s e n θ 2 d θ

1 2 ∫ 0 π 2 1 + s e n 2 θ + 2   s e n θ d θ

Lembrando que s e n 2 x = 1 - cos 2 ⁡ x

E lelmbrando que cos 2 ⁡ x = 1 2 1 + cos ⁡ 2 θ 2 . Teremos :

1 2 ∫ 0 π 2 3 2 + 2 s e n θ - cos ⁡ 2 θ 2 d θ

Passo 3

1 2 3 2 θ - 2 cos ⁡ θ - s e n 2 θ 4 0 π 2

3 π 8 + 1

Resposta

3 π 8 + 1

Exercícios de Livros Relacionados

Encontre a área da região cortada do primeiro quadrante pela curva r = 2 2 - s e n 2 θ 1 2 .
Uma pétala de rosa: Encontre a área delimitada por uma pétala da rosa r=12c o s( 3 θ ) .
Concha de caracol: Encontre a área da região delimitada pelo eixo x positivo e a espiral r= 4 θ 3 ,0≤ θ≤2 π . A região se assemelha a uma concha de caracol.
Encontre a área da região comum aos interiores das cardioides r=1+c o s ⁡ ( θ ) er=1–c o s ⁡ ( θ ) .