Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.4 - Ex. 29

Uma pétala de rosa: Encontre a área delimitada por uma pétala da rosa r   =   12   c o s   ( 3 θ ) .

Passo 1

Faaaala, cara! Tranquileba?

Fazendo o gráfico da função, temos:

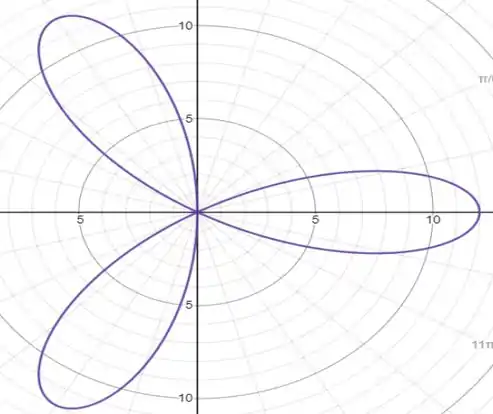
Que belezinha, não?! Tome para ti :P

Veja que podemos de maneira inteligente podemos facilitar a conta, veja que de r [0,12] o gráfico é simétrico em relação ao eixo x, de forma que podemos fazer o cálculo da área decima e multiplicar por 2.

Também (de maneira não aleatória) eu deixei o fundo do gráfico em graus, de forma que fica mais fácil par agente visualizar que a função vai de θ ∈ 0 , π 6

Passo 2

Por isto, temos:

A = 2 ∫ 0 π 6 ∫ 0 12 cos ⁡ 3 θ r   d r   d θ

2 ∫ 0 π 6 1 2 r 2 0 12 cos ⁡ 3 θ     d θ

2 ∫ 0 π 6 12 2 cos 2 ⁡ 3 θ 2   d θ

Sabendo que:  cos 2 ⁡ x = 1 2 1 + cos ⁡ 2 x

12 2 2 ∫ 0 π 6 ( 1 + c o s ⁡ ( 6 θ )   d θ

12 2 2 θ + s e n 6 θ 6 0 π 6

12 2 2 π 6 + 0 - 0 + 0

12 2 2 π 6

12 π

Resposta

A = 2 ∫ 0 π 6 ∫ 0 12 cos ⁡ 3 θ r   d r   d θ

A = 12 π

Exercícios de Livros Relacionados

Encontre a área da região cortada do primeiro quadrante pela curva r = 2 2 - s e n 2 θ 1 2 .
Cardioide no primeiro quadrante: Encontre a área da região cortada do primeiro quadrante pela cardioide r=1+s e n ( θ ) .
Concha de caracol: Encontre a área da região delimitada pelo eixo x positivo e a espiral r= 4 θ 3 ,0≤ θ≤2 π . A região se assemelha a uma concha de caracol.
Encontre a área da região comum aos interiores das cardioides r=1+c o s ⁡ ( θ ) er=1–c o s ⁡ ( θ ) .