Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.4 - Ex. 32

Encontre a área da região comum aos interiores das cardioides r   =   1   +   c o s ⁡ ( θ ) e   r   =   1   –   c o s ⁡ ( θ ) .

Passo 1

Faaaala, cara! Tranquileba?

Fazendo um esboço das funções, temos:

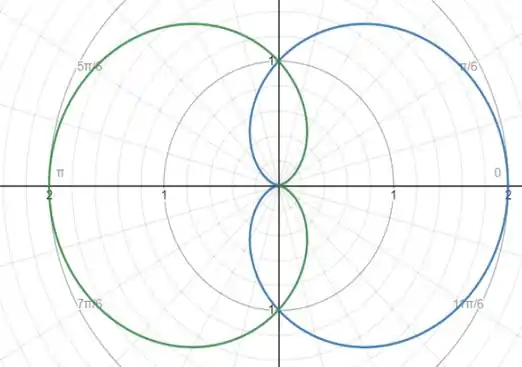
A área interior a qual queremos acha. Observe que há uma simetria. Você concorda comigo que se acharmos uma área podemos multiplicar por 4 e achar a área total que queremos.

Para explicar melhor:

Seria essa meia folha (pois é kkskss meia folha, parece, não?)

Se acharmos a área dela, e multiplicarmos por 4 chegamos ao resultado que queremos., ou seja, a área das 4 meia folhas.

Passo 2

Dando um super zoo, vemos que o ângulo começa do 0:

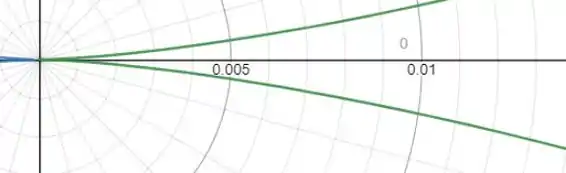
E como mostrado na primeira figura, esse ângulo se prossegue até π / 2 .

E para a curva que faz esse caminho:

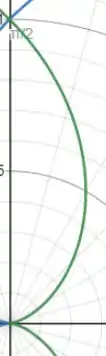
Essa verde, no caso, é a 1 - cos ⁡ θ

Passo 3

Diante de todos esses passos, podemos concluir que a integral será:

A = ∫ 0 π 2 ∫ 0 1 - cos ⁡ θ r   d r   d θ

∫ 0 π 2 1 2 r 2 0 1 - cos ⁡ θ d θ

∫ 0 π 2 1 - cos ⁡ ( θ ) 2 2   d θ

1 2 ∫ 0 π 2 1 + cos 2 ⁡ θ - 2 cos ⁡ θ d θ

Lembrando que cos 2 ⁡ x = 1 2 1 + cos ⁡ 2 x

1 2 ∫ 0 π 2 d θ + ( ∫ 0 π 2 1 2 d θ + ∫ 0 π 2 cos ⁡ 2 θ 2 d θ ) -   ∫ 0 π 2 2 cos ⁡ θ

1 2 θ + θ 2 + s e n 2 θ 4 - 2 s e n θ 0 π 2

1 2 π 2 + π 4 + 0 - 2 - 0

3 π - 8 2

Resposta

A = ∫ 0 π 2 ∫ 0 1 - cos ⁡ θ r   d r   d θ

E o valor da integral é:

3 π - 8 2

Exercícios de Livros Relacionados

Encontre a área da região cortada do primeiro quadrante pela curva r = 2 2 - s e n 2 θ 1 2 .
Uma pétala de rosa: Encontre a área delimitada por uma pétala da rosa r=12c o s( 3 θ ) .
Cardioide no primeiro quadrante: Encontre a área da região cortada do primeiro quadrante pela cardioide r=1+s e n ( θ ) .
Concha de caracol: Encontre a área da região delimitada pelo eixo x positivo e a espiral r= 4 θ 3 ,0≤ θ≤2 π . A região se assemelha a uma concha de caracol.