Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.4 - Ex. 18

Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar.

∫ - 1 1 ∫ - 1 - x 2 1 - x 2 2 1 + x 2 + y 2 d y   d x

Passo 1

Faaaala, cara! Tranquileba?

Das coordenadas polares temos que:

x = r cos ⁡ θ

y = r   s e n θ

x 2 + y 2 = r 2

E em caso de dúvidas, vejamos a figura para que possamos entender melhor.

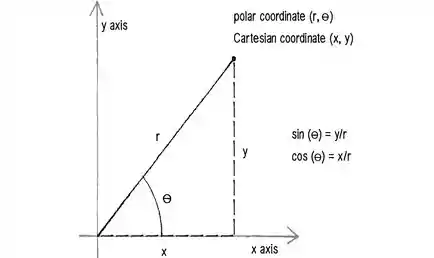
E em se tratando de integrais, quando transformamos uma integral para coordenadas polares, temos que adicionar o jacobiano das coordenadas polares, que no caso é r .

Passo 2

Não sei se lembra, meu/minha amigo[a], mas no capítulo anterior aprendemos a fazer o gráfico de uma função polar dado sua integral.

Em resumo, a primeira integral é a função geradora do gráfico, a segunda corresponde os pontos as funções se interceptam.

Neste caso temos as funções:

y = 1 - x 2

y - 1 - x 2

E se fizermos o esboço dessas funções, temos:

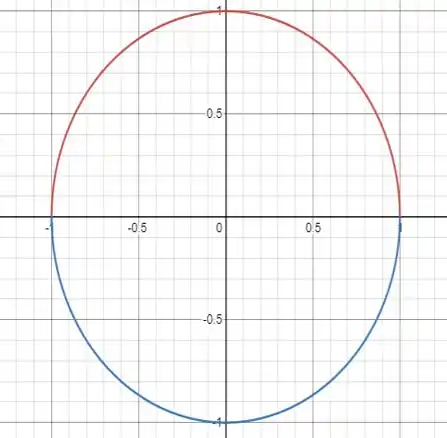
Dado que os limites de integração dados pela segunda integral são de [-1,1], temos que:

Se:

0 ≤ r ≤ 1

E se multiplicarmos por 4 obtemos o círculo completo

0 ≤ θ ≤ π 2

Feito isto, vamos para a função dada. Temos que:

2 1 + x 2 + y 2 2

Sabendo que:

x 2 + y 2 = r 2

2 1 + r 2 2

Passo 3

Assim:

∫ - 1 1 ∫ - 1 - x 2 1 - x 2 2 1 + x 2 + y 2 2 d y   d x = 4 ∫ 0 π 2 ∫ 0 1 2 1 + r 2 2 r   d r   d θ

Façamos u = 1 + r 2 , logo d u = 2 r d r . Temos que quando r = 0 ,   u = 1 e r = 1 ,   u = 2 . Portanto:

4 ∫ 0 π 2 ∫ 0 2 2 2 u 2   d u   d θ

4 ∫ 0 π 2 - 1 u 1 2 d θ

4 ∫ 0 π 2 - 1 2 + 1 d θ

4 2 θ 0 π 2

π

Resposta

∫ - 1 1 ∫ - 1 - x 2 1 - x 2 2 1 + x 2 + y 2 2 d y   d x = 4 ∫ 0 π 2 ∫ 0 1 2 1 + r 2 2 r   d r   d θ

E o valor da integral é:

π

Exercícios de Livros Relacionados

Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule ∫ ∫ D e x + y x - y x - y 2 d x d y , onde D = x , y ∈ R 2 1 ≤ x - y 2 ≤ 4 ,y ≤ 0ex + y ≥ 0
Calcule a integral dupla ∫ ∫ D d x d y p 2 + x 2 + y 2 p Onde: D = x , y ∈ R 2 x 2 + y 2 ≤ a 2 } .
Se a0 , seja I a = ∫ - a a e - u 2 d u .Calcule as integrais sobre B 1 e B 2 , e use b ) para mostrar que I a tende para π quando a tende para + ∞ . Isto prova que ∫ 0 + ∞ e - u 2 d u = π 2 .