Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.4 - Ex. 30

Concha de caracol: Encontre a área da região delimitada pelo eixo x positivo e a espiral r   = 4 θ 3 ,   0   ≤ θ   ≤   2 π . A região se assemelha a uma concha de caracol.

Passo 1

Faaaala, cara! Tranquileba?

Fazendo um esboço da função:

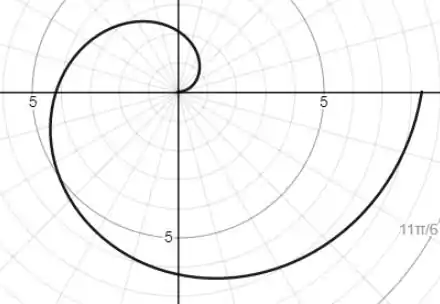
E dado pelo enunciao que:

0 ≤ θ ≤ 2 π

0 ≤ r ≤ 4 θ 3

Logo:

A = ∫ 0 2 π ∫ 0 4 θ 3 r   d r   d θ

Passo 2

∫ 0 2 π 1 2 r 2 0 4 θ 3 d θ

∫ 0 2 π 1 2 4 2 θ 2 3 2 d θ

2 3 3 2 ∫ 0 2 π θ 2   d θ

2 3 3 2 1 3 θ 3 0 2 π

2 3 3 3 2 3 π 3

2 6 π 3 3 3

Resposta

A = ∫ 0 2 π ∫ 0 4 θ 3 r   d r   d θ

E:

A = 2 6 π 3 3 3

Exercícios de Livros Relacionados

Encontre a área da região cortada do primeiro quadrante pela curva r = 2 2 - s e n 2 θ 1 2 .
Uma pétala de rosa: Encontre a área delimitada por uma pétala da rosa r=12c o s( 3 θ ) .
Cardioide no primeiro quadrante: Encontre a área da região cortada do primeiro quadrante pela cardioide r=1+s e n ( θ ) .
Encontre a área da região comum aos interiores das cardioides r=1+c o s ⁡ ( θ ) er=1–c o s ⁡ ( θ ) .