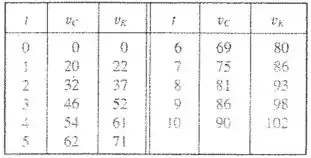
Os caros de corrida dirigidos por Cristina e Laís estão lado a lado na lagada de uma corrida. A tabela mostra as velocidades de cada carro (em milhas por hora) durante os primeiros 10s de corrida. Use a regra do ponto médio para estimar quão mais longe Laís viaja em relação a Cristina durante os primeiros 10 segundos;

Laís viaja aproximadamente 1 / 45 milhas a mais que Cristina nos primeiros 10 segundos.

Enunciado

Vamos lembrar do seguinte: qual é a relação entre velocidade, tempo e deslocamento?

Ou, em forma integral:

Isso quer dizer que, para estimar o deslocamento total em um certo intervalo de tempo, precisamos achar uma aproximação para essa integral.

Como queremos calcular a diferença nos deslocamentos de Laís e Cristina, vamos fazer:

Vamos chamar essa função de :

Agora vamos relembrar a regra do ponto médio. A primeira coisa a fazer é dividir o intervalo de em alguns trechos iguais.

Por exemplo, se dividirmos em trechos, teremos intervalos de cada.

Como as velocidade estão em milhas por hora, vamos reescrever em horas:

Para o método do ponto médio, nós vamos avaliar a função nos pontos médios de cada um dos intervalos de .

Ou seja, temos que avaliar a função em . Então a integral é:

Essa será, aproximadamente, a distância entre as duas após os primeiros .

Laís viaja aproximadamente milhas a mais que Cristina nos primeiros segundos.