Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.1 - Ex. 2

Encontre a área da região hachurada

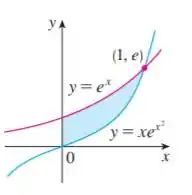
Passo 1

Eaee, belezinha?? Bom... queremos encontrar a área da seguinte região sombreada:

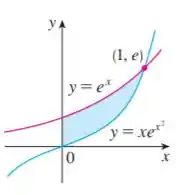
Para encontrarmos a área hachurada, basta integrarmos ( e m x o u y ) a função que está em cima (y = e^x) e subtrair pela função que está por baixo (y = x e^(x^2)) no intervalo dado.

Analisando a figura, percebemos que trata-se do intervalo de 1 a 0 . Em outras palavras, este será os nossos limites de integração!!

E aí?? Bora lá?? 😉

Ah, lembre-se que:

int u^n d u = (u^(n + 1))/(n + 1) + C

E

int e^u d u = e^u + C

Passo 2

Com base no que acabamos de falar, temos:

int_0^1 e^x - x * e^(x^2) d x = int_0^1 e^x d x - int_0^1 x * e^(x^2) d x

Resolvendo a primeira integral, temos:

int_0^1 e^x d x = e^x ([[1],[0]]) :.

int_0^1 e^x d x = e^1 - e^0 :.

int_0^1 e^x d x = e - 1

Agora vamos resolver a segunda integral!!

Passo 3

Resolvendo a segunda integral, temos:

int_0^1 x * e^(x^2) d x

Fazendo u = x^2 :. d u = 2 x d x , temos:

int_0^1 x * e^(x^2) d x = int_0^1 x * e^u (d u)/(2 x) :.

int_0^1 x * e^(x^2) d x = (1)/(2) int_0^1 e^u d u :.

int_0^1 x * e^(x^2) d x = (1)/(2) e^u ([[1],[0]]) :.

Substituindo u :

int_0^1 x * e^(x^2) d x = (1)/(2) e^(x^2) ([[1],[0]]) :.

int_0^1 x * e^(x^2) d x = (1)/(2) (e^(1^2) - e^0) :.

int_0^1 x * e^(x^2) d x = (e - 1)/(2)

Passo 4

Com isso, a nossa integral do Passo 2, fica:

int_0^1 e^x - x * e^(x^2) d x = int_0^1 e^x d x - int_0^1 x * e^(x^2) d x :.

int_0^1 e^x - x * e^(x^2) d x = (e - 1) - ((e - 1)/(2)) :.

int_0^1 e^x - x * e^(x^2) d x = (e - 1)/(2)

Entendeu direitinho?? Responde aee 😉

Resposta

(e - 1)/(2)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Avalie a integral e interprete-a como a área de uma região. Esboce a região ∫ - 1 1 | 3 x - 2 x | d x
Esboce a região delimitada pelas curvas fornecidas. Decida se quer integrar com relação a x ou y . Desenhe um retângulo aproximado típico e identifique sua altura e largura. Então, encontre a área da
Esboce a região delimitada pelas curvas fornecidas. Decida se quer integrar com relação a x ou y . Desenhe um retângulo aproximado típico e identifique sua altura e largura. Então, encontre a área da
Use um gráfico para encontrar as coordenadas x aproximadas dos pontos de interseção das curvas dadas. Então indique (aproximadamente) a área da região delimitada pelas curvas. y = 1,3 x ,y = 2 x
Esboce a região delimitada pelas curvas fornecidas e encontre sua área. y = 2 x 3 , y = x 2 / 8, 0 ≤ x ≤ 6