Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.1 - Ex. 31

Esboce a região delimitada pelas curvas fornecidas e indique sua área

y = x 1 + x 2 ,     y = x 2 1 + x 3

Passo 1

Opa, fala ae!! Beleza?? Antes de tudo, precisamos ver como essas funções ficam no gráfico.

Esboçando a região delimitada pelas curvas teremos o seguinte:

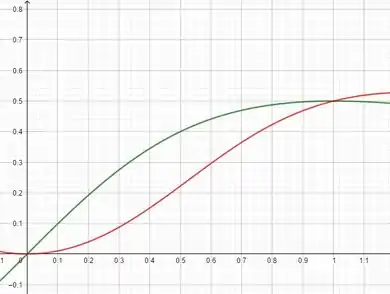
Onde, a função em verde é y = x 1 + x 2 e a função em vermelho é a y = x 2 1 + x 3 , ok? Com isso, podemos ver que elas se encontram em x = 0 e x = 1 . E a função debaixo sempre é a vermelha!

Assim, vamos integrar de 0   a   1 a função que está por cima menos a função que está por baixo, então, teremos

∫ 0 1 x 1 + x 2 - x 2 1 + x 3 d x = ∫ 0 1 x 1 + x 2 d x - ∫ 0 1 x 2 1 + x 3 d x

Vamos resolver uma de cada vez!

Passo 2

Primeiro:

∫ 0 1 x 1 + x 2 d x

Vamos usar a substituição u = 1 + x 2 → d u = 2 x d x , assim os limites serão x = 0 → u = 1 e x = 1 → u = 2 :

∫ 1 2 x u d u 2 x = 1 2 ∫ 1 2 1 u d u = 1 2 ln ⁡ u 1 2 =

= 1 2 ln ⁡ 2 - ln ⁡ 1 = ln ⁡ 2 2

Passo 3

Próxima integral:

∫ 0 1 x 2 1 + x 3 d x

Vai ser bem parecida com a última integral! Vamos fazer a substituição u = 1 + x 3 → d u = 3 x 2 d x e os limites serão x = 0 → u = 1 e x = 1 → u = 2 :

∫ 1 2 x 2 u d u 3 x 2 = 1 3 ∫ 1 2 1 u d u = 1 3 ln ⁡ u 1 2 =

= 1 3 ln ⁡ 2 - ln ⁡ 1 = ln ⁡ 2 3

Passo 4

Agora, é só juntar tudo na primeira expressão que tínhamos:

∫ 0 1 x 1 + x 2 - x 2 1 + x 3 d x = ∫ 0 1 x 1 + x 2 d x - ∫ 0 1 x 2 1 + x 3 d x

∫ 0 1 x 1 + x 2 - x 2 1 + x 3 d x = ln ⁡ 2 2 - ln ⁡ 2 3 =

= 3 ln ⁡ 2 - 2 ln ⁡ 2 6

∴

= ln ⁡ 2 6 ≈ 0,115524

Resposta

ln ⁡ 2 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use um gráfico para encontrar as coordenadas aproximadas x dos pontos de intersecção das curvas dadas. A seguir, encontre a área aproximada da região limitada pelas curvas y = xs e nx 2 ,y = x 4
Encontrar a área da região limitada pelas curvas dadas. y = ln ⁡ x ,x = 1ey = 4
Encontrar a área da região limitada pelas curvas dadas. y = 1 x + 1 ,y = 1 x ,y = 2 x + 1ex = - 3
Encontrar a área da região limitada pelas curvas dadas. y = x - 2ey = 2 - x - 2 2
Calcular a área da parte da circunferência x = 2 cos ⁡ t y = 2s e nt Que está acima da reta y = 1 .