Esboce a região delimitada pelas curvas fornecidas e indique sua área
Passo 1
Esboçando a região delimitada pelas curvas para teremos o seguinte
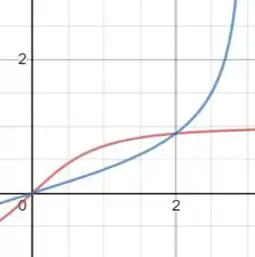
Assim, vamos integrar de a função que está por cima menos a função que está por baixo, então, teremos
Esboce a região delimitada pelas curvas fornecidas e indique sua área
Esboçando a região delimitada pelas curvas para teremos o seguinte

Assim, vamos integrar de a função que está por cima menos a função que está por baixo, então, teremos