Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 150

Carretel para cabos

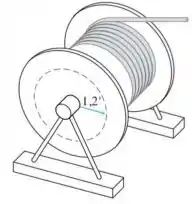
Um cabo de televisão é puxado de um grande carretel para ser colocado nos postes telefônicos da rua. Ele é desenrolado do carretel, onde está disposto em camadas de raio constante (veja a figura a seguir). Se o caminhão que puxa o cabo se desloca a uma velocidade constante de 6   p é s / s (pouco mais de 4   m i l h a s / h o r a ), use a equação s   =   r θ para determinar a que taxa ( em radianos por segundo) o carretel gira enquanto a camada de raio 1,2 pé é desenrolada.

Passo 1

A velocidade com que o caminhão puxa o cabo é uma taxa do espaço em um intervalo de tempo podendo ser representada por d s / d t = 6   p é s / s . Suponhamos que s, r e θ sejam deriváveis em t e sabendo que a camada de raio do carretel r = 1,2   p é é constante. A taxa com a qual o carretel gira (em radianos por segundo) é igual a d θ / d t .

Passo 2

s = r θ

d s d t = r d θ d t + θ d r d t  

Como r é uma constante, sabemos que d r / d t = 0 . Logo:

d s d t = r d θ d t

Passo 3

Com os dados fornecidos pelo enunciado do exercício e substituindo-os na última equação:

6 = 1,2 d θ d t

d θ d t = 5

Resposta

No momento em questão, o carretel gira a uma taxa de 5   r a d / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água está sendo armazenada em um reservatório cônico (vértice para baixo). Supondo que a água evapora a uma taxa proporcional à área da superfície exposta ao ar, mostre que sua profundidade irá decres
Uma partícula move-se ao longo de uma curva cuja equação é: x y 3 1 + y 2 = 8 5 Suponha que a coordenada x esteja crescendo a uma taxa de 6u n i d a d e sp o rs e g u n d o quando a partícula estiver
Um meteorito entra na atmosfera da Terra e queima a uma taxa que, em cada instante, é proporcional à área de sua superfície. Supondo que o meteorito é sempre esférico, mostre que o raio decresce a uma
Uma partícula move-se ao longo da curva y= x x 2+1 . Encontre todos os valores de x nos quais a taxa de variação de x em relação ao tempo é três vezes a de y . [Suponha que d x / d t nunca é nula.]
A equação das lentes finas em Física é: 1 s + 1 S = 1 f onde s é a distância do objeto à lente, S é a distância da imagem à lente e f é a distância focal da lente. Suponha que uma certa lente tenha um