Água está sendo armazenada em um reservatório cônico (vértice para baixo). Supondo que a água evapora a uma taxa proporcional à área da superfície exposta ao ar, mostre que sua profundidade irá decrescer a uma taxa constante que não depende das dimensões do reservatório.
Passo 1
Vamos falar que a água dentro do reservatório forma um cone com altura , raio e volume .
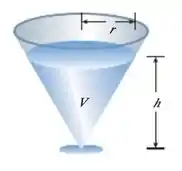
De forma que pela fórmula do volume do cone podemos falar que:
Passo 2
Como o enunciado fala sobre a velocidade com que profundidade muda, parece útil derivarmos essa expressão em relação ao tempo, pra aparecer o que representa exatamente o que nos interessa. Fazendo isso fica assim:
Usando a regra da derivada do produto, vamos ter:
Pela regra da cadeia:
Chegamos que
Passo 3
Mas aí apareceu um tal de que não temos e nem estamos interessados, mas podemos derivar a tangente do ângulo do vértice do cone pra relacionar ele com
Como o ângulo não varia:
Passo 4
Mas o que significa falar que que a água evapora a uma taxa proporcional à área da superfície exposta ao ar? A taxa com que a água evapora nada mais é do que a taxa de variação do volume, e essa taxa é proporcional a área da superfície exposta ao ar:
Aonde é a constante de proporcionalidade.
Passo 5
Agora vamos juntar todas as nossas equações:
Substituindo (2) e (3) em (1) pra deixar tudo em função de :
Esse é um momento que a gente fica muito triste, porque fizemos tudo certinho, mas o ainda ta dependendo de e . Masss lembra que ?? Bora jogar isso ali dentro:
Opaaa opaaa está provado o que o enunciado pediu, constante que não depende das dimensões do reservatório.
Resposta
Ei, a resposta está no passo a passo :)