Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.6 - Ex. 12
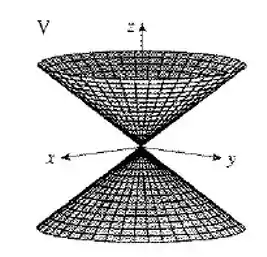
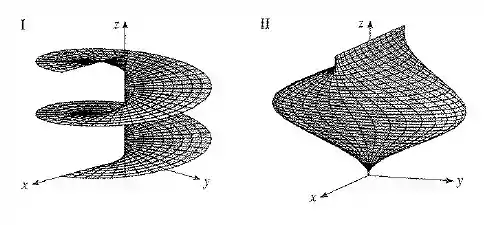
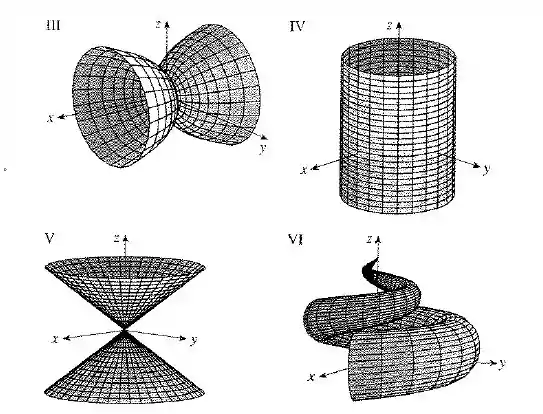
Case as equações com os gráficos identificados por e dê razões para sua resposta. Determine quais famílias de curvas da grade têm constante e quais têm constante.
Passo 1
E aiiiiiiii minha turma, beleza!?
Bom, nesse exercício temos que analisar a parametrização abaixo, e identificar qual dos gráficos de que ela representa. Não esquecendo de justificar a sua escolha.
Temos que a parametrização é:
Para resolver essa questão, devemos analisar a parametrização dada.
Repare que temos:
Qual a ideia agora? Você deve associar essa parametrização com a de um círculo em coordenadas polares.
Repare que no plano , temos uma parametrização típica de um círculo.
Agora eu quero que você faça essa comparação. Aí você vai compreender que temos um círculo de raio no plano , e como pode assumir qualquer valor de u, vamos gerar um cone no plano .
Agora, bora lá resolver essa!!
Passo 2
Começamos relembrando a parametrização de um círculo, ou melhor, sua representação em coordenadas polares.
Para um círculo, temos que:
E sua parametrização:
Comparando com a parametrização dada:
Temos que:
Assim, repare que conseguimos concluir que:
Logo,
Passo 3
Repare que realmente temos um círculo no plano .
Porém, esse círculo varia conforme o raio , assim como a posição no eixo que também depende de .
Dessa forma, vamos ter vários círculos em torno do eixo z que vão aumentando de tamanho conforme se afastamos da origem, formando um cone. Desse jeito:
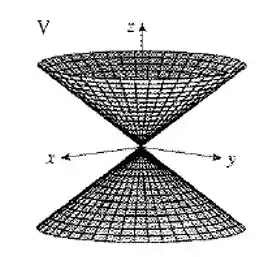
As curvas de grade com constantes são os círculos horizontais que vemos, correspondentes as equações no plano . Se for constante, são múltiplos escalares de , correspondente às curvas da grade de linha reta através da origem.
Resposta
