Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.6 - Ex. 30

Determine as equações paramétricas da superfície obtida pela rotação da curva x = 4 y 2 - y 4 , - 2 ≤ y ≤ 2 em torno do eixo y e use-as para traçar o gráfico da superfície.

Passo 1

Vamos usar a representação da forma paramétrica da superfície de revolução:

x = f y cos ⁡ θ               y = y             z = f y sen ⁡ θ

Vamos substituir f y = 4 y 2 - y 4 :

x = 4 y 2 - y 4 cos ⁡ θ               y = y             z = 4 y 2 - y 4 sen ⁡ θ

Com - 2 ≤ y ≤ 2 e 0 ≤ θ ≤ 2 π .

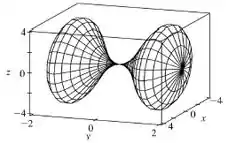
E aqui está o gráfico da superfície:

Resposta

x = 4 y 2 - y 4 cos ⁡ θ               y = y             z = 4 y 2 - y 4 sen ⁡ θ ;     - 2 ≤ y ≤ 1 ,       0 ≤ θ ≤ 2 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja σ u , v = ( x , y , z ) , com x = u cos ⁡ v , y = us e nv e z = u .Mostre que a transformação σ transforma a reta u = u 1 ( u 1 ≠ 0 constante) numa circunferência. Desenhe tal circunferência no c
Seja sigma (u , v , w) = ( u cos v , u s e n v , w ) , 0 = u = 1 , 0 = v = 2 pi e 0 = w = 1 . Desenhe a imagem de sigma .
Seja σ a transformação do exercício anterior. Verifique que σ transforma o retângulo 0 ≤ u ≤ 1, 0 ≤ v ≤ 2π e w = 1, em um círculo. Desenhe tal círculo.
Considere a transformação σ (θ, ρ, φ) = (x, y, z) onde x = ρ sen φ cos θ, y = ρ sen φ sen θ e z = ρ cos φ.Desenhe σ (B) onde B é o conjunto ρ = ρ 1 ( ρ 10 constante), 0 ≤ θ ≤ 2π e 0 ≤ φ ≤ π.Desenhe σ
(Coordenadas esféricas) Seja P = ( x , y , z ) e considere a terna ( θ ,ρ ,φ ) onde θ é o ângulo entre o semieixo positivo O x e o vetor O P 1 → = ( x , y , 0 ) , ρ o comprimento do vetor O P → e φ o