Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.6 - Ex. 26
Use um sistema algébrico computacional para produzir um gráfico que se pareça com o que está dado.
Passo 1
E aiiiiii turma, tudo beleza!?
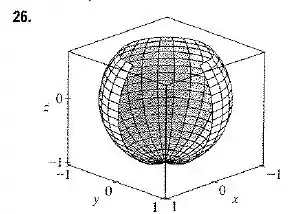
Nessa questão nosso objetivo é reproduzir um gráfico que se pareça com a figura a seguir:
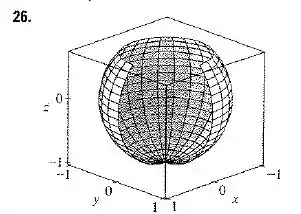
Utilize um software para fazer a representação.
Vamos avaliar essa figura juntos!
Eu quero que você analise a figura com calma, e perceba que ela lembra muito uma porção de esfera, certo!
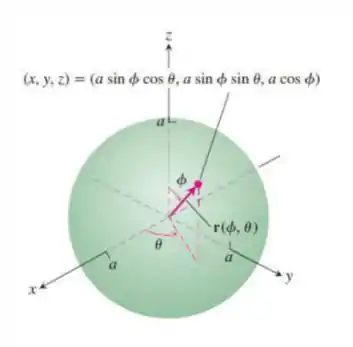
Veja que temos uma esfera de raio com centro na origem. E perceba também que a variação dos ângulos não são completos. Veja a figura abaixo:
Nessa figura, a variação dos ângulos está para uma esfera completa. No nosso caso, ela não é completa.
Agora, eu quero que você encontre uma parametrização para a esfera.
Depois que você achar essa parametrização, utilize o Geogebra 3D para plotar o gráfico. Ai faça uma comparação entre as figuras.
Importante, como a esfera não é completa você pode assumir um intervalo de ângulos desse jeito por exemplo:
Vamos nessa!
Passo 2
Já vimos que a uma geometria que pode representar a figura é a esfera.
Vamos achar uma parametrização para a esfera.
Vamos ter o seguinte:
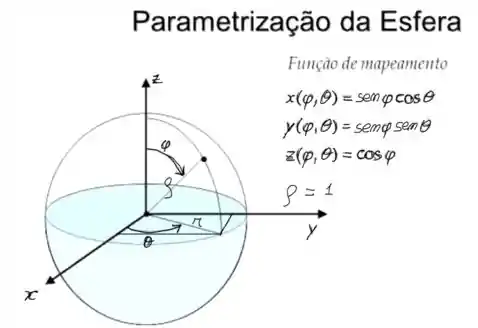
Apenas escrevendo em outra notação, temos:
Com as restrições:
Passo 3
Agora que temos a parametrização, podemos plotar essa superfície com o auxílio do Geogebra 3D.
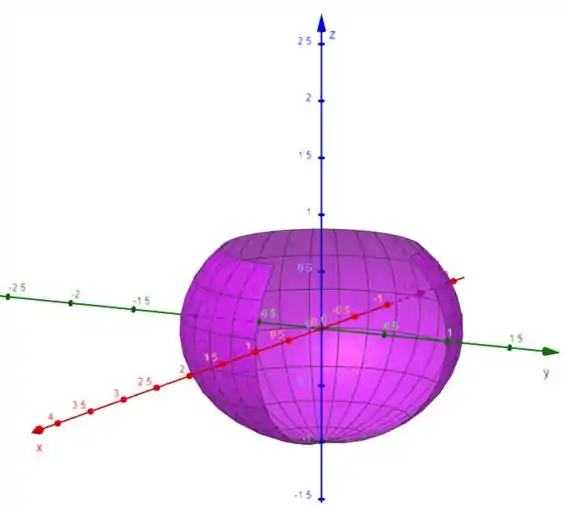
Fazendo isso temos:
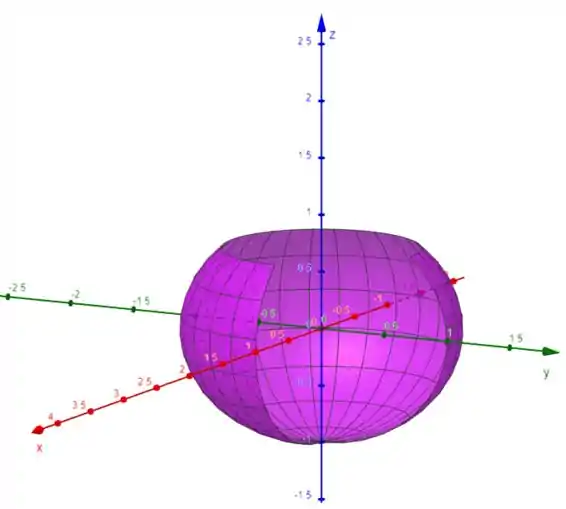
Caso queira plotar, use esse input:
a=Superfície(sen(u) cos(v),sen(u) sen(v),cos(u),v,((π)/(2)),2 π,u,((π)/(4)),π)
É só você copiar e colar no Geogebra 3D.
Compare os dois gráficos! Observe que realmente encontramos uma figura muito parecida, logo, podemos concluir que uma esfera pode ser uma parametrização.
Resposta
