Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.6 - Ex. 11
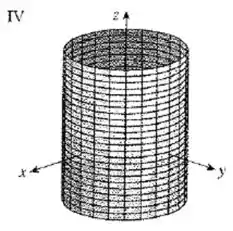
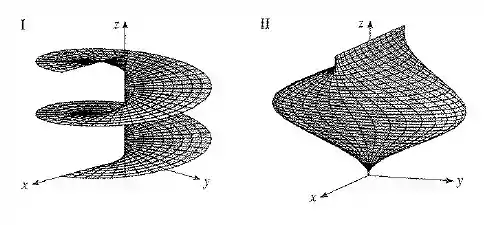
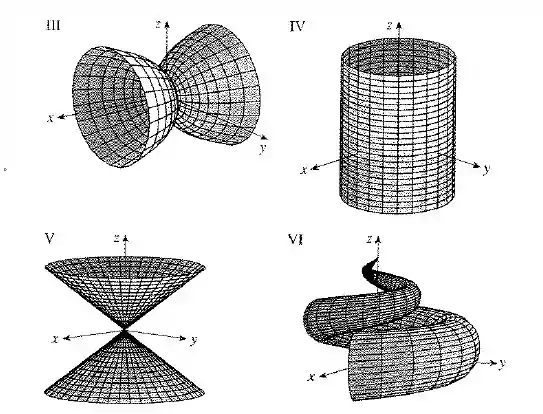
Case as equações com os gráficos identificados por e dê razões para sua resposta. Determine quais famílias de curvas da grade têm constante e quais têm constante.
Passo 1
Faaala pessoal, belezinha!
Nessa questão devemos analisar a parametrização abaixo, e identificar qual dos gráficos de que ela representa. Não esquecendo de justificar a sua escolha.
Temos que a parametrização é:
Para resolver essa questão, devemos analisar a parametrização dada.
Repare que temos:
A ideia agora, é você associar essa parametrização com a de um círculo em coordenadas polares.
Repare que no plano , temos uma parametrização típica de um círculo.
Agora eu quero que você faça essa comparação. Aí você vai compreender que temos um círculo de raio no plano , e como pode assumir qualquer valor, vamos gerar um cilindro no plano .
Bora lá resolver essa!!
Passo 2
Vamos começar relembrando a parametrização de um círculo, ou seja, sua representação em coordenadas polares.
Para um círculo:
Temos que,
Comparando com a parametrização dada:
Temos que:
Assim, conseguimos perceber que o raio vale:
Logo,
Passo 3
Assim, podemos concluir que realmente temos um círculo de raio no plano .
E conforme vamos assumindo valores para u:
Vamos ter círculos com centro em cada valor de , isso vai acabar gerando um cilindro que tem o eixo central como o .
Olhando para as figuras dadas no enunciado, a que representa esse tipo de curva é o gráfico :
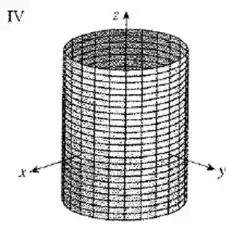
As curvas da grade com raio constante são os círculos horizontais que vemos no plano . Se é constante, ambos são constantes, com variação livre.
Resposta
