Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.6 - Ex. 25
Determine uma representação paramétrica para a superfície.
A parte do cilindro que está entre os planos e
Passo 1
Faaaaala galera, beleza!?
Nessa questão devemos achar uma parametrização para a seguinte expressão:
que está entre os planos:
Para essa questão galera, observe bem a expressão dada e compare com a expressão de um círculo em um plano :
O segredo parte daí, porque conhecemos uma parametrização para círculo. Que é:
Com,
Mas repare que esse circulo está variando no eixo , entre e . E isso acaba gerando um cilindro no espaço tridimensional, desse jeito:
Utilize essas informações para parametrizar a expressão dada!
Agora vou deixar o resto com você!
Bora lá!
Passo 2
Sabemos que a expressão dada tem a cara de um círculo no plano :
Observe que o raio vale 4, pois temos que:
Para um círculo, temos a seguinte parametrização
Onde,
Mas como ele nos deu que em , o eixo perpendicular a esse círculo estamos variando de:
Vamos ter a seguinte parametrização:
Teremos um cilindro, desse jeito:
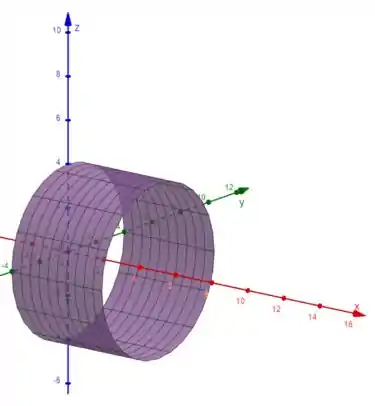
Essa figura foi feita a partir da parametrização no Geogebra 3D com o seguinte input:
a=Superfície(u,4 cos(v),4 sen(v),v,0,2 π,u,0,5)