Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 26
Determine uma representação paramétrica para a superfície.
A parte do plano que está dentro do cilindro
Passo 1
Fala, galera!
Precisamos fazer uma representação paramétrica da superfície definida pelo plano
Que está dentro do cilindro
Podemos ver através desse gráfico a superfície que estamos procurando:
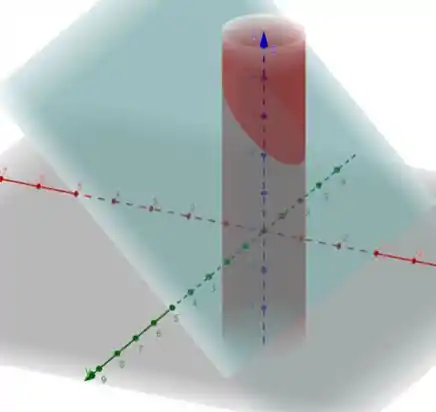
Como estamos trabalhando com um cilindro, podemos converter tudo para coordenadas polares, onde
Passo 2
Temos então que:
Vamos substituir o plano :
É simples ver que vai de a e vai de a .
Assim as equações paramétricas serão:
Resposta
Exercícios de Livros Relacionados
Identifique a superfície que tem a equação paramétrica dada. r → x , θ = x , cos θ ,s e nθ
Faça uma correspondência entre as equações e os gráficos identificados por I - V I e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u ,
Identifique a superfície que tem a equação paramétrica dada. r x , θ = x , x cos θ , x sen θ
Faça uma correspondência entre as equações e os gráficos identificados por I-VI e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u , v
Faça uma correspondência entre as equações e os gráficos identificados por I-VI e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u , v