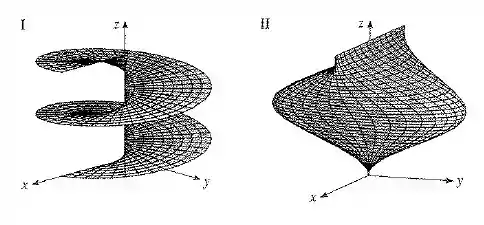
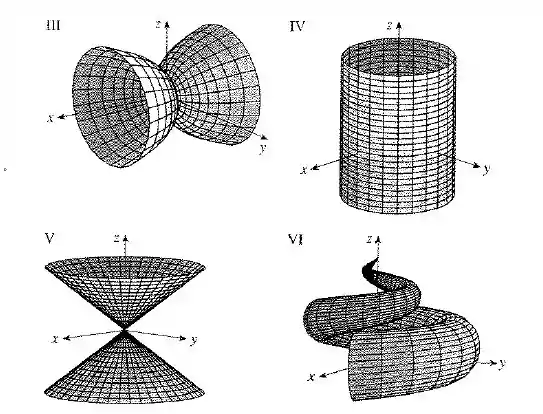
Case as equações com os gráficos identificados por e dê razões para sua resposta. Determine quais famílias de curvas da grade têm constante e quais têm constante.

, ,

Bom, então estamos lidando com as seguintes equações paramétricas:

Como , não existe restrição para esse valor, então nossa superfície varia livremente no eixo . Se olharmos o gráfico de vemos que a superfície varia em torno do eixo , então já podemos excluir a possibilidade de ser a superfície que estamos procurando.

Como é constante:

e

São constantes.

Como varia linearmente, controla a rotação no plano . Isso sugere pra gente que nossa superfície é helicoidal (ou seja, em formato de hélice, de espiral).

Como é o argumento da função e nas nossas equações paramétricas, temos que:

Então, quando toma todos os valores possíveis, e completam um ciclo completo no plano, isso faz com que se formem círculos perfeitos e elipses, já que temos constantes de multiplicando nas nossas equações paramétricas.

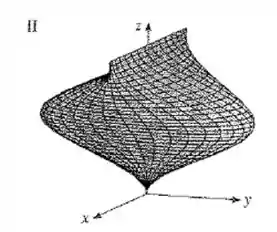
Então, nosso gráfico onde varia livremente, e e rotaciona em torno de com círculos e elipses é o gráfico .

Determinando quais famílias de curvas da grade têm constante e quais têm constante:

• Se for mantido constante e fornecer uma equação de elipse no plano , as curvas da grade são elipses orientadas horizontalmente.

Observe que quando , a 'elipse' é o ponto único e, quando temos enquanto intervalos que variam de a um segmento de linha paralelo ao eixo no plano . Essa é a "costura" superior que vemos no gráfico .

• Quando é mantido constante, é livre para variar; portanto, as curvas de grade correspondentes são as curvas que vemos correndo para cima e para baixo ao longo da superfície, ou seja, curvas helicoidais.