Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 5
Identifique a superfície dada a equação vetorial
Passo 1
Fala pessoal, para analisar a superfície precisamos achar a equação parametrizada para facilitar a compreensão.
Para isso vamos igualar as componentes da equação a uma função.
Sendo assim :
Para analisar a superfície vamos precisar encontrar a relação de . Podemos ver que dependem de , logo o primeiro passo que teremos que fazer é escrever essas equações sem esses parâmetros, para podermos analisar com mais facilidade.
E analisar graficamente como elas seriam, beleza?
Passo 2
Vamos começar tirando os parâmetros das equações:
Como vimos , , podemos substituir nas duas equações:
Show, então o parâmetro sumiu. Agora precisamos pensar em como sumir com o parâmetro . Eita, como podemos fazer isso?
Uma maneira de sumir com e e tentar achar . Esse é um bizu que podemos usar em vários tipos de questões.
Bom , então vamos começar elevando cada equação ao quadrado:
Somando as duas equações:
Opa, já está ficando com o formato que a gente quer. Vamos por em evidência:
Perfeito galera, conseguimos sumir com o parâmetro também.
Passo 3
Beleza pessoal, então a nossa equação é:
Essa é uma equação padrão para representar um cone . Logo desenhado graficamente teremos:
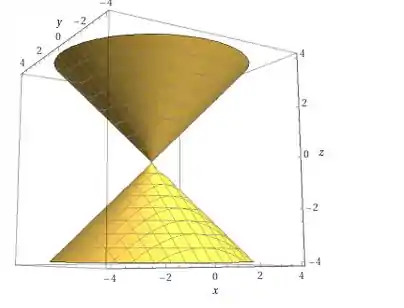
Resposta
A superfície é um cone.