Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.2 - Ex. 73

73. Centroide Determine o centroide da região delimitada pelos gráficos de y = x + cos ⁡ x e

y = 0 para 0 ≤ x ≤ 2 π .

Passo 1

O exercício se refere a essa região

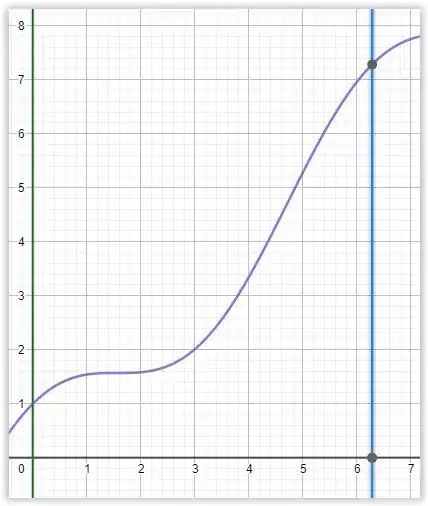
E temos que determinar o centroide.

O centroide é o centro geométrico, ou o centro de massa se houver uma distribuição homogênea de densidade.

Passo 2

Vamos começar calculando a massa total.

A massa é a integral da curva

M = ∫ 0 2 π   ( x + cos ⁡ x ) d x  

∫ 0 2 π   x + cos ⁡ x d x = ∫ 0 2 π   x   d x + ∫ 0 2 π cos ⁡ x   d x

∫ 0 2 π   x   d x = x 2 2 0 2 π = 4 π 2 2 = 2 π 2

∫ 0 2 π cos ⁡ x   d x = s e n   2 π - s e n   0 = 0 - 0 = 0

Então nossa massa é

M = ∫ 0 2 π   x + cos ⁡ x d x =   2 π 2  

Passo 3

Agora vamos calcular nosso ponto médio em x

X m = ∫ 0 2 π x ⋅ d m ∫ 0 2 π d m = 1 2 π 2 ∫ 0 2 π x ⋅ x + cos ⁡ x d x = 1 2 π 2 ∫ 0 2 π x 2 + xcos ⁡ x d x

Passo 4

Agora temos que calcular essa integral

1 2 π 2 ∫ 0 2 π x 2 + xcos ⁡ x d x = 1 2 π 2 ∫ 0 2 π x 2 d x + ∫ 0 2 π x c o s   x   d x  

Primeiro vamos resolver essa integral

∫ 0 2 π x 2 d x = x 3 3 0 2 π = 8 3 π 3

Agora vamos resolver a outra integral

∫ 0 2 π x c o s   x   d x  

Vamos fazer uma integral por partes

∫ u d v = u v - ∫ v d u

Onde

u = x d u = d x d v = cos ⁡ x v = s e n   x

Isso vai nos dar que

∫ 0 2 π x c o s   x   d x   = [ x ⋅ s e n   x ] 0 2 π - ∫ 0 2 π s e n   x   d x

E sabemos que

∫ 0 2 π s e n   x   d x = - [ cos ⁡ x ] 0 2 π

Então

∫ 0 2 π x c o s   x   d x   = [ x ⋅ s e n   x ] 0 2 π + [ cos ⁡ x ] 0 2 π = 0 - 0 + 1 - 1 = 0

Logo

X m = 1 2 π 2 ∫ 0 2 π x 2 + xcos ⁡ x d x = 1 2 π 2 ⋅ 8 3 π 3 + 0 = 8 6 π = 4 3 π

Passo 5

Agora temos calcular o ponto médio em y

Y m = ∫ 0 2 π y ⋅ d m ∫ 0 2 π d m = 1 2 π 2 ∫ 0 2 π 1 2 ⋅ x + cos ⁡ x 2 d x = 1 4 π 2 ∫ 0 2 π ( x 2 + 2 ⋅ x ⋅ cos ⁡ x + c o s 2 x ) d x

Passo 6

Agora vamos calcular essa integral

1 4 π 2 ∫ 0 2 π ( x 2 + 2 ⋅ cos ⁡ x + c o s 2 x ) d x = 1 4 π 2 ∫ 0 2 π x 2 d x + ∫ 0 2 π 2 x ⋅ cos ⁡ x d x + ∫ 0 2 π c o s 2 x   d x

Vamos calcular as integrais separadamente

∫ 0 2 π x 2 d x = x 3 3 0 2 π = 8 π 3 3

Agora a segunda integral

∫ 0 2 π 2 x ⋅ cos ⁡ x d x = 2 ∫ 0 2 π x ⋅ cos ⁡ x d x

Opa! A gente já calculou essa integral antes, isso aqui vai dar 0 .

A última integral agora

∫ 0 2 π c o s 2 x   d x

Vamos usar a seguinte identidade trigonométrica

c o s 2 ѳ = 1 + c o s ⁡ ( 2 ѳ ) 2

Então

∫ 0 2 π c o s 2 x   d x = ∫ 0 2 π 1 2   d x + ∫ 0 2 π c o s ⁡ ( 2 x ) d x

Vamos calcular todas essas integrais

∫ 0 2 π 1 2   d x = 1 2 2 π - 0 = π

Agora a segunda integral

∫ 0 2 π c o s ⁡ ( 2 x ) d x

Vamos fazer a substituição em que

u = 2 x d u = 2 d x

∫ 0 2 π c o s ⁡ ( 2 x ) d x = 1 2 ∫ 0 4 π c o s ⁡ ( u ) d u = 1 2 s e n   4 π - s e n   0 = 0

Então

∫ 0 2 π c o s ⁡ ( 2 x ) d x = π - 0 = π

Agora podemos somar

Y m = 1 4 π 2 ∫ 0 2 π ( x 2 + 2 ⋅ cos ⁡ x + c o s 2 x ) d x = 1 4 π 2 8 π 3 3 + 0 + π = 8 π 3 + 3 π 12 π 2 = 8 π 2 + 3 12 π

Resposta

Nosso ponto médio ficaria   4 3 π   ,     8 π 2 + 3 12 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Use a fórmula de redução no Exemplo 6 para mostrar que: ∫ s e n ²x . d x = x 2 - s e n2 x 4 + C ² (b) Use a parte (a) e a fórmula de redução para calcular ∫ s e n 4x . d x .
Use integração por partes para demonstrar a fórmula da redução. tg n ⁡ x d x = tg n - 1 ⁡ x n - 1 - ∫ tg n - 2 ⁡ x d x( n ≠ 1 )
Demonstre que, para as potências de seno, ∫ 0 π 2 se n 2 n ⁡ x d x = 3 * 5 * 7 * … * 2 n - 1 2 * 4 * 6 * … * 2 n π 2
Demonstre a fórmula de redução ∫ cos n ⁡ x d x = 1 n cos n - 1 ⁡ x se n ⁡ x + n - 1 n ∫ cos n - 2 ⁡ x d x Use a parte (a) para calcular ∫ cos 2 ⁡ x d x . Use as partes (a) e (b) para calcular ∫ cos 4
Use a fórmula de redução do Exemplo 6 para mostrar que ∫ 0 π 2 se n n ⁡ x d x = n - 1 n ∫ 0 π 2 se n n - 2 ⁡ x d x Use a parte (a) para calcular ∫ 0 π 2 se n 3 ⁡ x d x e ∫ 0 π 2 se n 5 ⁡ x d x .Use a