Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.1 - Ex. 47

(a) Use a fórmula de redução no Exemplo 6 para mostrar que:

∫ s e n ²   x . d x = x 2 - s e n   2 x 4 + C

(b) Use a parte (a) e a fórmula de redução para calcular ∫ s e n 4   x . d x .

Passo 1

Bom galera, antes de começar vamos lembrar do que o Exemplo 6 nos diz:

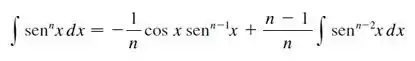
Usando a fórmula, e sabendo que n = 2 só precisamos substituir:

∫ s e n ²   x . d x = - 1 2 . cos ⁡ x . s e n 2 - 1 x + 2 - 1 2 ∫ s e n 2 - 2   x . d x

∫ s e n ²   x . d x = - 1 2 . cos ⁡ x . s e n   x + 1 2 ∫ s e n 0   x . d x

∫ s e n ²   x . d x = - 1 2 . cos ⁡ x . s e n   x + 1 2 ∫ 1 . d x

Resolvendo:

∫ s e n ²   x . d x = - 1 2 . cos ⁡ x . s e n   x + x 2

Precisamos lembrar que:

s e n   2 x = 2 . s e n   x . cos ⁡ x

Isolando s e n   x . cos ⁡ x :

s e n   x . cos ⁡ x = s e n   2 x 2

Agora é só substituir:

∫ s e n ²   x . d x = - 1 2 . s e n   2 x 2 + x 2

Então:

∫ s e n ²   x . d x = x 2 - s e n   2 x 4

Agora só falta adicionar a constante:

∫ s e n ²   x . d x = x 2 - s e n   2 x 4 + C

Prontinho!!

Passo 2

Na letra b fazemos a mesma coisa mas usamos n = 4 :

∫ s e n 4   x . d x = - 1 4 . cos ⁡ x . s e n 4 - 1 x + 4 - 1 4 ∫ s e n 4 - 2   x . d x

∫ s e n 4   x . d x = - 1 4 . cos ⁡ x . s e n 3 x + 3 4 ∫ s e n 2   x . d x

Substituindo aqui o resultado da letra a:

∫ s e n 4   x . d x = - 1 4 . cos ⁡ x . s e n 3 x + 3 4 x 2 - s e n   2 x 4

∫ s e n 4   x . d x = - 1 4 . cos ⁡ x . s e n 3 x + 3 8 x - 3 16 s e n   2 x

Adicionamos a constante:

∫ s e n 4   x . d x = - 1 4 . cos ⁡ x . s e n 3 x + 3 8 x - 3 16 s e n   2 x + C

Resposta

  1. ∫ s e n ²   x . d x = x 2 - s e n   2 x 4 + C ;
  2. ∫ s e n 4   x . d x = - 1 4 . cos ⁡ x . s e n 3 x + 3 8 x - 3 16 s e n   2 x + C .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Avalie a integral. ∫ t sin ² ⁡ t d t ²
Avalie a integral. ∫ tan 2 ⁡ θ sec 4 ⁡ θ d θ
Calcule a integral. ∫ cos ⁡ θ cos 5 ⁡ ( s e nθ )d θ
Determine o volume gerado pela rotação de um arco da curva y = s e n x em torno do eixo das abscissas.
Nos exercícios 1 a 35 , calcular a integral indefinida.