Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.5 - Ex. 12
a) Encontre o valor médio de no intervalo dado.
b) Encontre tal que .
c) Esboce o gráfico de e um retângulo cuja área é a mesma que a área sob o gráfico de .
Passo 1
E aí, galerinha! 😁
Nesse problema foi dada a função e dentro do intervalo queremos obter o valor medio de , obter de modo que e esboçar o gráfico de e um retângulo cuja área é a mesma que a área sob o gráfico de
Parece complicado? 🤔
Para obter o valor medio de uma função fazemos
E para obter , fazemos e igualamos ao valor que encontramos em .
Sacou? Bora lá! 😉
Passo 2
a) Encontrando o valor médio com sendo e
Aplicando o método de substituição
Temos que , então
Calculando a integral e aplicando os limites de integração
Tranquilo até aqui? 😉
Passo 3
Fazendo , temos
E por fim, fazendo o esboço do gráfico de , temos
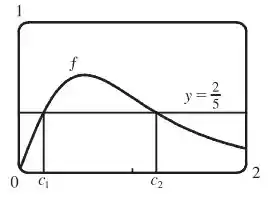
E aí! O que achou? Responde Aí! 😁
Resposta
- ou
- Gráfico