Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.5 - Ex. 21

Use o resultado do Exercício 79 na Seção 5.5 para calcular o volume médio de ar inalado pelos pulmões em um ciclo respiratório.

Passo 1

Bom galera, o Exercício 79 na seção 5.5 nos diz que a taxa de fluxo de ar para dentro dos pulmões é calculado como:

f t = 1 2 s e n   2 π t 5

E que o volume, nessas condições ao longo de um tempo t é dado por:

V t = 5 4 π 1 - cos ⁡ 2 π t 5

Como queremos o volume médio teremos que calcular o valor médio da função. Mas como?

Basta usarmos:

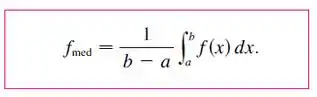
Tranquilo, não é? O Exercício 79 também nos disse que um ciclo respiratório consiste em 5 segundos, então vamos integrar a função de 0 até 5, tudo bem?

Só vamos substituir:

V m e d = 1 5 - 0 ∫ 0 5 5 4 π 1 - cos ⁡ 2 π t 5 . d t

Tiramos as constantes:

V m e d = 1 5 . 5 4 π ∫ 0 5 1 - cos ⁡ 2 π t 5 . d t

Separando a função:

V m e d = 1 4 π ∫ 0 5 1 . d t - ∫ 0 5 cos ⁡ 2 π t 5 . d t

A primeira integral é fácil, não é?

V m e d = 1 4 π t - ∫ 0 5 cos ⁡ 2 π t 5 . d t

A próxima teremos que resolver por substituição:

u = 2 π t 5

Derivando:

d u = 2 π 5 . d t → 5 2 π d u = d t

Substituímos:

V m e d = 1 4 π t - ∫ 0 5 cos ⁡ u . 5 2 π d u

V m e d = 1 4 π t - 5 2 π ∫ 0 5 cos ⁡ u . d u

Resolvendo:

V m e d = 1 4 π t - 5 2 π s e n   u | 5 0

Substituindo u:

V m e d = 1 4 π t - 5 2 π s e n   2 π t 5 | 5 0

Aplicando o intervalo:

V m e d = 1 4 π 5 - 5 2 π s e n   2 π × 5 5 - 0 - 5 2 π s e n   2 π × 0 5 | 5 0

V m e d = 1 4 π 5 - 5 2 π s e n   2 π - - 5 2 π s e n   0

V m e d = 1 4 π 5 - 5 2 π × 0 - - 5 2 π × 0

V m e d = 5 4 π ≅ 0,4   L

Resposta

V m e d = 0,4   L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade v do sangue que circula em uma veia com raio R e comprimento l a uma distância r do eixo central é v r = P 4 η l ( R 2 - r 2 ) Onde P é a diferença de pressão entre as extremidades da vei
Use o diagrama para mostrar que se f é côncava para cima em [ a , b ] , então f m e df a - b 2
Se uma xícara de café tem uma temperatura de 95°C em uma sala cuja temperatura ambiente é de 20°C , de acordo com a lei do resfriamento de Newton, a tempertatura do café após t minutos será T t = 20 +
Use o resultado do Exercicio 77 na seção 5.5 para calcular o volume médio de ar inalado pelos pulmões em um ciclo respiratório.
A velocidade de um carro é lida de seu velocímetro em intervalos de 10 segundos e registrada na tabela. Use a Regra do Ponto Médio para estimar a distância percorrida pelo carro.