Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 65
Em uma certa província, a velocidade máxima permitida em estradas é de e a velocidade mínima é . A multa por violar esses limites é de por cada quilometro por hora acima da velocidade máxima ou abaixo da velocidade mínima. Expresse a quantidade de multa como uma função da velocidade de condução e esboce o gráfico de para .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente construir uma expressão para a quantidade de multa em função da velocidade de condução de um veículo. Em seguida, esboçar essa função em um gráfico, considerando o intervalo .
Pra isso, ele nos disse que a velocidade máxima permitida é de , que a velocidade mínima é de e que a multa por violar esses limites é de por cada quilometro por hora acima da velocidade máxima ou abaixo da velocidade mínima.
Perceba que se você passar um quilometrozinho por hora a mais ou a menos, você já pagará a multa né? Então, precisaremos dividir a multa em dois casos, para caso seja abaixo da mínima e para caso seja acima da máxima. Assim, vamos traduzir esses dados matematicamente e construir a nossa expressão.
Vamos lá!
Passo 2
Na primeira situação, a multa é 10 vezes a diferença entre a velocidade mínima permitida, de , e a velocidade que o motorista estava. Assim, temos:
Da mesma forma, quando a velocidade for acima do limite de , temos:
Mas e se o motorista estiver entre as velocidades permitidas?
Então, ele não leva multa e devemos considerar na nossa função.
Passo 3
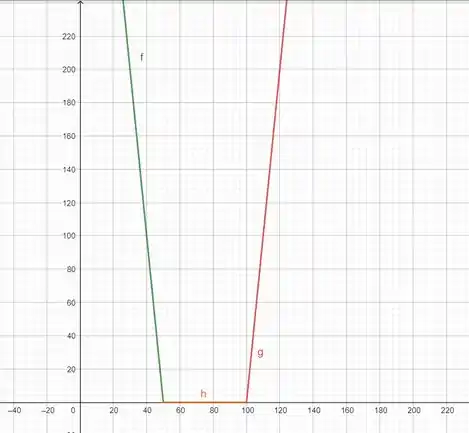
Agora juntando tudo e organizando a função de acordo com a velocidade de condução , temos:
Passo 4
Esboçando a função, temos:
Valeu, galera! Até a próxima! 😉