Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.4 - Ex. 18

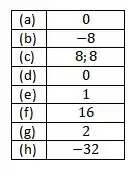
18 Se uma pedra for atirada verticalmente para cima com uma velocidade inicial, e t s e o sentido positivo é pra cima. Ache:

(a) a velocidade média da pedra no intervalo de tempo 3 4 ≤ t ≤ 5 4 ;

(b) a velocidade instantânea da pedra em t = 3 4 s e em t = 5 4 s;

(c) a velocidade escalar da pedra em t = 3 4 s e em t = 5 4 s;

(d) a velocidade média da pedra no intervalo de tempo 1 2 ≤ t ≤ 3 4 ;

(e) quantos segundos irão decorrer ate que que a pedra chegue ao chão;

(f) qual a altura máxima atingida;

(g) quantos segundos irão decorrer ate que a pedra chegue ao chão;

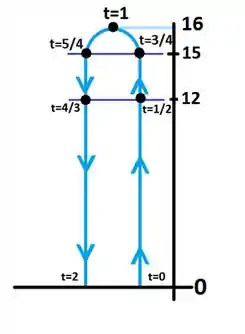
(h) a velocidade instantânea da pedra quando ela atingir o solo. Mostre o comportamento do movimento através de uma figura similar à figura 3

Passo 1

Bom gente, o conceito que tá sendo trabalhado aqui é o seguinte, a altura de alguma coisa que está no chão é zero bem tranquilo né. Se essa função descreve o movimento de uma pedra, que é lançado do chão o referencial é o chão, ou seja, o valor onde a função é zero, onde a altura dela é zero, outro conceito importante é, tudo que sobe desce então essa pedra vai atingir o chão novamente, ou seja vai atingir altura zero.

Passo 2

Para velocidade segue o mesmo do ensino médio.

(a)

s = - 16 t 2 + 32 t

v m = ∆ s ∆ t = s 5 4 - s 3 4 5 4 - 3 4 = - 16 5 4 2 + 32 ⋅ 5 4 - - 16 3 4 2 + 32 ⋅ 3 4 1 2 = 0

Passo 3

Como já vimos nos exercícios anteriores a velocidade e a derivada de da função deslocamento

(b)

v t = d s d t = - 32 t + 32

v 3 4 = - 32 ⋅ 3 4 + 32 = 8 ;     v 5 4 = - 32 ⋅ 5 4 + 32 = - 8

Passo 4

Bom aqui você pode se perguntar qual a diferença entre velocidade instantânea e escalar, a velocidade instantânea tem sentido, modulo e direção, em outras palavras é uma grandeza vetorial, no caso da velocidade escalar nós queremos apenas o modulo.

(c)

v e t = v t

v e 3 4 = v 3 4 = 8 = 8 ;     v e 5 4 = v 5 4 = - 8 = 8

Passo 5

Mais velocidade média:

(d)

v m = ∆ s ∆ t = s 3 4 - s 1 2 3 4 - 1 2

s 3 4 = - 16 3 4 2 + 32 . 3 4 = - 16.9 16 + 32.3 4 = + 15

s 1 2 = - 16 1 2 2 + 32 . 1 2 = - 16 4 + 32 2 = + 12

v m = 15 - 12 0,25 = 12 m / s

Passo 6

A pedra começa a descer após atingir sua altura máxima, momento em que atinge a altura máxima sua velocidade é zero, então basta encontrar o momento em que a velocidade se anula.

e)

v t = 0 ⟺ - 32 t + 32 = 0 ⟹ t = 1

Passo 7

Como t = 1 é o ponto onde a altura é máxima basta substituir em s ( t ) :

(f)

s 1 = - 16 ⋅ 1 2 - 32 = 16

Passo 8

Já para encontrarmos o o tempo que demora para que a pedra caia teremos que igualar s ( t ) a zero.

(g)

s t = 0 ⟺ - 16 t 2 + 32 t = 0 ⟹ t - 16 t + 32 = 0 ⟹ t = t 1 = 0 t 2 = 2

Passo 9

Ahhhh finalmente está acabando tudo que precisamos agora é substituir t = 2 em v ( t )

h)

v 2 = - 32 ⋅ 2 + 32 = - 32

Agora que já temos os pontos e valores importantes sobre o movimento da pedra podemos marcar esses valores em um gráfico.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Durante os meses de verão, Terry faz e vende colares na praia. No verão passado, ele vendeu os colares por $10 cada e suas vendas eram em média de 20 por dia. Quando ele aumentou o preço $1 , descobri
Um time de beisebol joga em um estádio com capacidade para 55000 espectadores. Com o preço do ingresso a $10 , a frequência média tem sido de 27000 . Quando os ingressos abaixaram para$8 , a frequênci
Um fabricante tem vendido 1000 aparelhos de televisão por semana, a $450 cada. Uma pesquisa de mercado indica que para cada $10 de desconto oferecido ao comprador, o número de aparelhos vendidos aumen
O gerente de um complexo de apartamentos com 100 unidades sabe, a partir da experiência, que todas as unidades estarão ocupadas se o aluguel for$ 800 por mês. Uma pesquisa de mercado sugere que, em mé
O gráfico mostra o consumo de combustível c de um carro (medido em litros/hora) como uma função da velocidade v do carro. Em velocidade muito baixa, o motor não rende bem; assim, inicialmente c decres