Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.8 - Ex. 33a
Um circuito elétrico simples consiste em um resistor de R ohms, onde R = 1 + 0,001t em ts com t variando entre [0,500]. O resistor é ligado em serie com o capacitor de 0,1 farad e uma força eletromotriz de 80 V . A carga q coulombs e a corrente é i ampers em ts. Se a carga no capacitor for 4 coulombs
- Expresse q como função do tempo
- Expresse i como função do tempo
- Ache a carga maxima
Passo 1
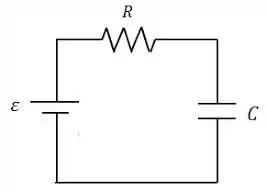
A figura 1 mostra um exemplo de circuito RL. Se a gente usar a Lei das malhas Podemos dizer que :
Passo 2
Podemos reescrever essa equação como
Essa é uma equação não homogênea, então não temos como usar o truque de separar variáveis. O jeito mais fácil é resolver por Fator Integrante. (Se estiver com duvida como prosseguir, da uma olhadinha na teoria. Temos uma seção especial só falando de fator integrante )
Entao se tivermos uma equação no formato
podemos usar um fator integrante , definido por
Passo 3
No nosso caso b(t) =
g(t) =
Logo
Vamos Multiplicar ambos os lados da nossa equação por
Da uma olhada no lado esquerdo e como ele parece uma regra da cadeia. Percebeu ?
Entao vamos reescrever nossa equação
Pronto, agora a parte difícil já foi resolvida. Vamos usar e integrar ambos os lados
Podemos simplificar essa exponencial
Entao nossa equação fica
O lado direito fica
Essa integral fica fácil fácil se fizermos substituição
U =
du = 0,01 dt
Agora unindo as expressões
Lembrando que fizemos uma integral indefinida, então temos que acrescentar uma constante arbitraria , C.
Perfeito. Encontramos nossa equação para a Carga.
Agora Achando C , pelos dados de contorno
Q(0) = 4
Assim