Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.4 - Ex. 17

Velejando. Um veleiro se move ao longo de uma reta, e o vento lhe fornece uma força constante de 50 libras na direção do movimento. A única outra força que age sobre o barco é a resistência à medida que o barco se move na água. A força de resistência é numericamente igual a cinco vezes a velocidade do barco, e a velocidade inicial é 1   p é / s . Qual é a velocidade máxima do barco em pés por segundo sob a ação desse vento?

Passo 1

Para entendermos o que está acontecendo façamos um diagrama de corpo livre com nosso corpo de massa m . Assim, teremos

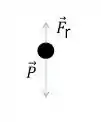
Na situação do problema como a bolinha de massa m está caindo temos que F = 50 - F r   e lembrando que F = m ⋅ a e que a força de resistência F r é numericamente igual a cinco vezes a velocidade do barco ( 5 ⋅ v ), dessa forma, podemos fazer

m ⋅ a = 50 -   5 ⋅ v

Passo 2

Agora, que temos a equação que modela e a condição inicial do mesmo, devemos lembrar que a = d v d t e faremos

m ⋅ d v d t = 50 - 5 ⋅ v

Dividindo todo mundo por m

d v d t = 1 m ⋅ ( 50 - 5 ⋅ v )

A velocidade máxima ocorre nos pontos críticos, ou seja, d v d t = 0 . Assim,

1 m ⋅ 50 - 5 ⋅ v = 0

50 - 5 ⋅ v = 0

5 ⋅ v = 50

v = 50 5 = 10   p é s / s

Resposta

10   p é s / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce uma parte do campo de direções da equação. Em seguida, adicione ao seu desenho a curva integral que passa pelo ponto P = ( 1 , - 1 ) . Use o método de Euler com x 0 = 1 e d x = 0,2 para estimar
Esboce uma parte do campo de direções da equação. Em seguida, adicione ao seu desenho a curva integral que passa pelo ponto P = ( 1 , - 1 ) . Use o método de Euler com x 0 = 1 e d x = 0,2 para estimar
35. Velocidade de escape. A força de atração gravitacional F exercida pela Lua sem ar sobre um corpo de massa m a uma distância s do centro da Lua é dada pela equação a seguir: F = - m g R 2 s - 2 , o
Identifique os valores de equilíbrio. Quais são estáveis e quais são instáveis?Construa a reta de fase. Identifique os sinais de y' e y" y ' = y - y
As equações diferenciais autônomas nos Exercícios 9-12 representam modelos de crescimento populacional. Em cada exercício, use a análise da reta de fase para esboçar curvas integrais P ( t ) , selecio