Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.4 - Ex. 16
Resistência proporcional a . Um corpo de massa é disparado verticalmente para baixo com velocidade inicial . Suponha que a força de resistência seja proporcional à raiz quadrada da velocidade e determine a velocidade terminal a partir de uma análise gráfica.
Passo 1
Para entendermos o que está acontecendo façamos um diagrama de corpo livre com nosso corpo de massa . Assim, teremos
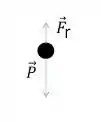
Na situação do problema como a bolinha de massa está caindo temos que e lembrando que e que a força de resistência é proporcional a raiz quadrada da velocidade (, dessa forma
Tendo, ainda,
Passo 2
Agora, que temos a equação que modela e a condição inicial do mesmo, devemos lembrar que e faremos
Dividindo todo mundo por
Fazendo
Nosso é, então, nossa velocidade terminal. Assim, Se
O objeto cairá cada vez mais rápido se aproximando da velocidade terminal, agora se
O objeto diminuirá e se afastará da velocidade terminal.