24. Um cocho tem de comprimento, e suas extremidades tem a forma de triângulos isósceles com de base e de altura. Se o cocho for preenchido com água a uma taxa de , quão rápido estará se elevando o nível da água quando ela tiver de profundidade?

Opa, bora lá! Essa questão fala de um cocho enchendo de água. Se você não sabe o que é um cocho ele é um recipiente que é usando pra vacas e bois se alimentarem ou beberem água. O nosso tem esse formato aqui:

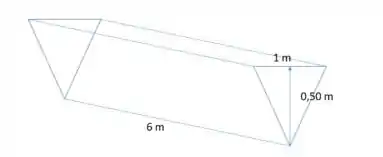
Temos um prisma triangular reto, cujo volume se dá pela área da base vezes a altura, então:

A área do triângulo que forma a base do cocho é:

Então, o volume é:

Para em metros.