Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 24
O cocho visto na figura a seguir será construído com as dimensões indicadas. Apenas o ângulo pode variar. Que valos de maximiza o volume do cocho?
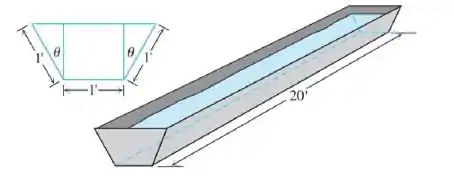
Passo 1
O volume vai ser a área da base vezes , como vimos na figura:
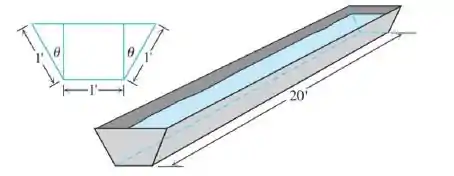
Se olharmos a base como dois triângulo de lado e ângulo , junto com um retângulo de lado e altura , conseguimos achar essa área da seguinte forma:
Falta acharmos o , para isso, vamos usar a trigonometria:
Assim:
E a área da base ficará:
Lembrando que
Vamos encontrar:
O vai de até
Passo 2
Para acharmos o valor de mínimo ou máximo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.
Derivando:
Fazendo isso igual a
Cortando o
Temos que fazer:
Usando
Vamos ter:
Resolvendo usando bhaskaas,
Assim
O segundo valor está fora do intervalo, vamos fazer
Passo 3
Vamos achar o valor da função nos pontos críticos e extremos do intervalo:
Vamos ter:
O maior dos valores é quando