Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 33
Determine as dimensões do retângulo de maior área que pode ser inscrito no triângulo retângulo mostrado na figura a seguir.
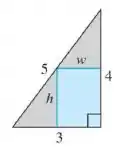
Passo 1
Vamos ter que a área do retângulo vai ser:
Olhando o triângulo retângulo, Vamos ter que o triângulo menor que está acima do retângulo é semelhante ao triângulo
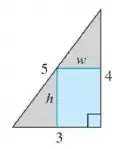
Sua base é e a altura é , logo:
Isso nos diz que:
E a área vai ficar:
Onde o valor máximo que pode assumir é e o mínimo é
Passo 2
Para acharmos o valor de mínimo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.
Começando por achar os pontos críticos:
Vamos derivar e achar:
Fazendo isso igual a
Passo 3
Vamos achar o valor da função nos pontos críticos e extremos do intervalo:
O maior dos valores é quando
Entao o retângulo tem dimensões:
Resposta
Exercícios de Livros Relacionados
Um fabricante de caixas deve produzir uma caixa sem tampa com um volume de 288c m ³ ³, onde a base é um retângulo com um comprimento três vezes maior que a largura. Ache as dimensões da caixa fabricad
Numa dada comunidade, uma certa epidemia alastra-se de tal forma que x meses após o seu início, P % da população estará infectada, onde P = 30 x 2 ( 1 + x 2 ) ² ². Em quantos meses o número de pessoas
Um fabricante de caixas deve produzir uma caixa fechada com um volume de 288c m ³ ³, onde a base é um retângulo com um comprimento três vezes maior que a largura. Ache as dimensões da caixa fabricada
Uma página deve conter 24c m ² ² de impressão com margens de 1 1 2c m em cima e embaixo, enquanto devemos ter 1c m de cada lado. Quais as dimensões da menor página que satisfaz todos esses requsiitos?
Para a lata do exemplo 4, suponha que o custo do material da tampa e da base seja o dobro do custo dos lados. Ache a altura e o raio da base para que o custo do material seja mínimo.