Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.5 - Ex. 67
Coeficientes angulares no gráfico da função tangente: Esboce em apenas um gráfico e sua derivada em . O gráfico da função tangente parece ter um coeficiente angular mínimo? E máximo? Em algum momento o coeficiente angular é negativo? Justifique suas respostas.
Passo 1
Esta é uma questão que necessita de recursos tecnológicos. Precisamos obter os gráficos da função tangente e da sua derivada no intervalo de variando entre . A partir destes gráficos, precisamos fazer múltiplas interpretações. Para a análise da nossa questão fluir bem, precisamos entender muito bem um ponto: como obtemos numericamente o coeficiente angular de uma reta?
O valor do coeficiente angular de uma função nada mais é do que a imagem da derivada dessa função. Isto é, se temos uma função , os valores são os coeficientes angulares da função no ponto .
Agora que relembramos este conceito, vamos direto as contas!
Passo 2
Primeiramente, vamos obter a derivada da função . Sendo assim, temos:
Passo 3
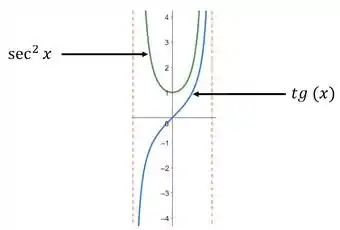
Vamos agora obter a curva das funções e no intervalo . Sendo assim, temos:
Passo 4
Agora que obtemos os gráficos, vamos extrair todas as informações possíveis. Para isto, estudaremos a imagem da função . Como podemos observar pelo gráfico, a imagem é o conjunto . Logo, possui um ponto de mínimo e não possui máximo. Sendo assim, temos:
- A função tangente possui um coeficiente angular mínimo igual a 1;
- Ela não possui coeficiente angular máximo, visto que tende ao infinito;
- Em nenhum momento o valor de é negativo. Portanto, a função tangente não possui coeficiente angular negativo (ela é estritamente crescente).
Resposta
A função tangente possui coeficiente angular mínimo igual a 1 e não possui valor máximo. Além disto, o coeficiente nunca é negativo.