Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 33

  1. Se f x = x 4 + 2 x , encontre f ' ( x )
  2. Verifique se sua resposta na parte (a) foi razoável comparando os gráficos de f e f ' .

Passo 1

Fala aí! como vai? 😎

Nesse problema foi dada a função

f x = x 4 + 2 x

E o nosso objetivo é determinar f ' x e comparar os gráficos de f e f ' para analisarmos se faz sentido a nossa derivação.

Parece complicado? 🤔

Iremos utilizar a equação abaixo para encontrarmos a derivada:

f ' x = lim h → 0 ⁡ f x + h - f x h

E para a criação do gráfico iremos utilizar o GeoGebra, por ser grátis, fácil e online.

Bora começar! 😎

Passo 2

Então, primeiro vamos tomar f ( x + h ) e f ( x ) :

f x + h = x + h 4 + 2 x + h

f x = x 4 + 2 x

Agora substituindo:

f ' x = lim h → 0 ⁡ ( x + h ) 4 + 2 x + h - x 4 - 2 x h

Calculando o termo a quarta potência e realizando a distributiva:

f ' x = lim h → 0 ⁡ x 4 + 4 x 3 h + 6 x 2 h 2 + 4 x h 3 + h 4 + 2 x + 2 h - x 4 - 2 x h

Simplificando termos semelhantes:

f ' x = lim h → 0 ⁡ 4 x 3 h + 6 x 2 h 2 + 4 x h 3 + h 4 + 2 h h

E agora simplificando o h :

f ' x = lim h → 0 ⁡ ( 4 x 3 + 6 x 2 h + 4 x h 2 + h 3 + 2 )

Aplicando o limite, chegamos em

f ' x = 4 x 3 + 2

Tranquilo até aqui? 😇

Passo 3

Esboçando os gráficos, ficamos com:

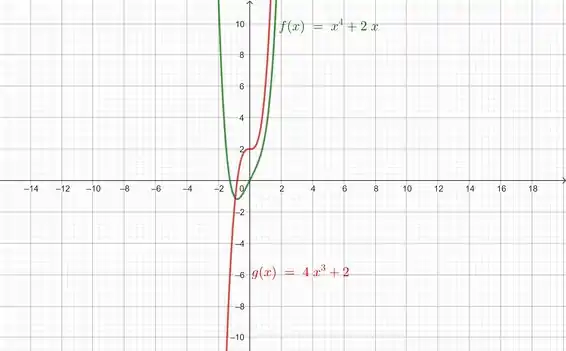
Onde a gente representou f ' ( x ) como g x apenas para fins didáticos.

f tem uma inclinação negativa íngreme à esquerda de   x   =   - 1   , então (   f ' ) tem valores negativos grandes correspondentes.

f ' muda de negativo para positivo conforme   f   muda de decrescente para crescente logo à direita de   x   =   - 1   .

Logo antes e depois de   x   =   0   ,   f   é quase reta como uma linha, então   f ' está muito próxima de um único valor ao mesmo tempo.

Na extremidade direita,   f   sobe com uma inclinação positiva crescentemente íngreme, e   f ' aumenta consequentemente.

  f ' parece razoável como a derivada de   f   .

E aí! entendeu tudo? Responde Aí! 😎

Resposta

  1. f ' x = 4 x 3 + 2
  2. Em comparação com o gráfico a aproximação foi razoável
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

55. Se y = x n , onde n é qualquer inteiro positivo, prove, por indução matemática, que d n d x n = n !
53. Se f ' , g ' , f ' ' e g ' ' existem, e se h =f° g , expresse h ' ' x em termos das derivadas de f e g .
Nos exercícios de 46 a 49, ache as fórmulas para f ' ( x ) e f ' ' ( x ) e estabeleça os domínios de f ' e f ' ' .48. f x = x 3
Nos exercícios de 46 a 49, ache as fórmulas para f ' ( x ) e f ' ' ( x ) e estabeleça os domínios de f ' e f ' ' . 49 . .f x = x 5 x , x ≠ 0 0 , x = 0
Nos exercícios de 46 a 49, ache as fórmulas para f ' ( x ) e f ' ' ( x ) e estabeleça os domínios de f ' e f ' ' . 46 .f x = x 2 x , x ≠ 0 0 , x = 0