Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.8 - Ex. 36
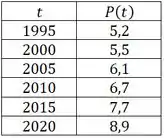
Seja a porcentagem da população das Filipinas com idade maior que anos no instante . A tabela fornece projeções dos valores desta função de a .
Qual o significado de ? Quais são as suas unidades?
Construa uma tabela de valores para
Faça os gráficos de e
Passo 1
E aí como vai? 😬
Nesse problema foi dada uma tabelinha com os valores da população com mais de anos das Filipinas de até . Os valores dados são esses aqui:
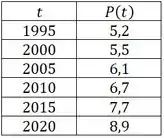
O item a) do enunciado pede pra explicarmos o significado de , a derivada de .
Além disso, de acordo com o item b), também precisamos usar esses valores de e pra pra construir uma tabela pra .
E por fim, pra fechar o item c), precisamos fazer um esboço do gráfico e .
Para obter as derivadas de valores discretos como nesse caso, podemos simplificar a definição de derivada. Olha só:
Olha só que interessante. Isso significa que podemos aproximar a derivada, calculado a razão das diferenças entre os valores discretos consecutivos que temos na tabela. Vamos ver como fazer isso juntos.
Bora começar! 😉
Passo 2
Em primeiro lugar, vamos atacar o item a) e tentar entender o significado de .
Pra isso, precisamos lembrar que a derivada de uma função representa a sua taxa de variação. Ou seja, nesse caso o seria a taxa na qual a porcentagem da população das Filipinas com idade maior que 60 anos está mudando ao longo do tempo.
Uma maneira um pouco mais concreta de enxergar isso é lembrar que se a porcentagem dessa população aumentar, será positivo. Consequentemente, se esse porcentagem diminuir, sera negativo.
Baseado nessa interpretação, a unidade de será %/ano.
Passo 3
O item b) pede pra construirmos uma tabela com valores pra . Vamos relembrar os valores de dados:
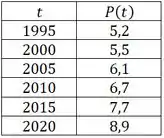
Vamos calcular as estimativas dos valores da derivada com a simplificação:
Vamos começar calculando o valor de . Como esse é um dos extremos, só conseguimos usar as informações dos pontos e . Olha só:
Vamos calcular agora para . Agora conseguimos usar o ponto anterior e o seguinte pra calcular as estimativas e usar a média entre os dois. Olha só:
Calculando a média, temos:
Agora só precisamos repetir esse processo pra todos os pontos:
Para :
Calculando a média, temos:
Para :
Calculando a média, temos:
Para :
Calculando a média, temos:
Para , calculamos usando apenas as informações em e :
Com esses valores calculados, conseguimos construir a tabela:
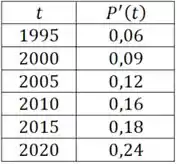
Tranquilo até aqui? 😉
Passo 4
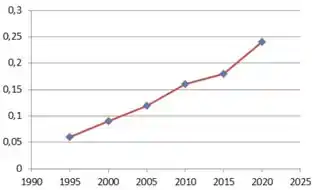
Pra fechar o item c), precisamos traçar os gráficos de e . Como as escalas são bem diferentes, vamos fazer um gráfico pra cada um.
Gráfico de :
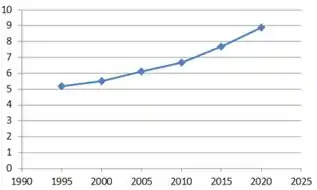
Gráfico de :
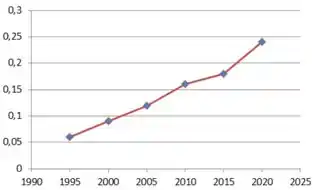
Ufa! Conseguimos terminar!
Resposta
a) é a taxa na qual a porcentagem da população das Filipinas com idade maior que 60 anos está mudando em relação ao tempo. Sua unidade é %/ano.
b)
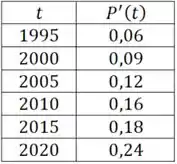
c)
Gráfico de :
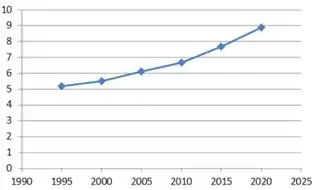
Gráfico de :
